20 Is What Percent Of 36
Kalali
Apr 17, 2025 · 5 min read
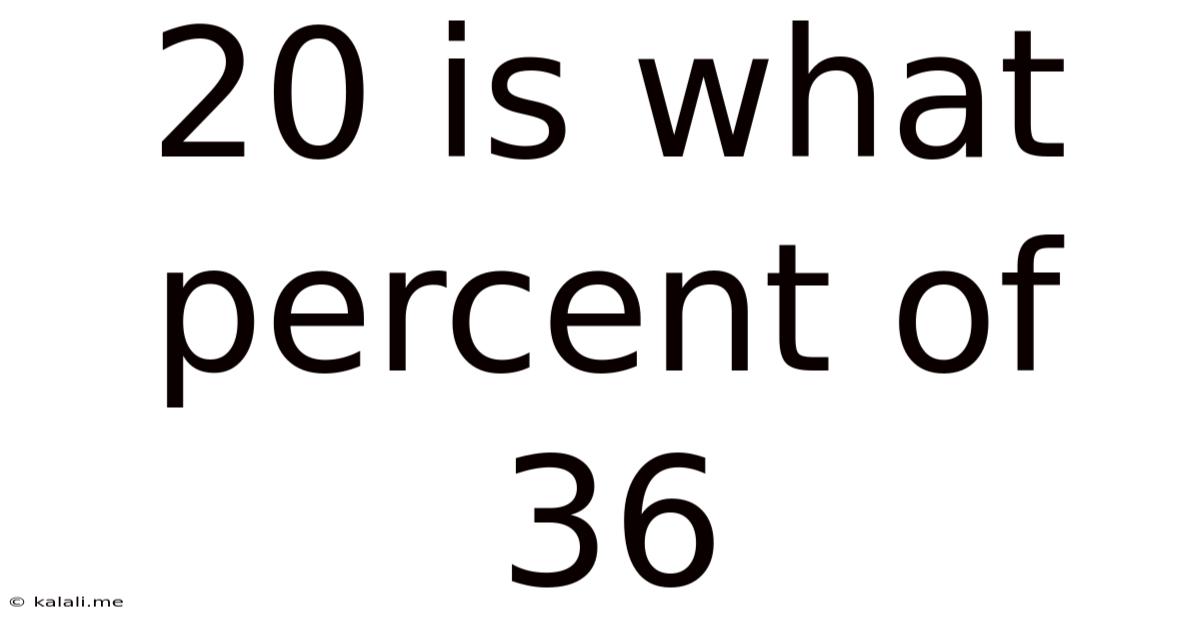
Table of Contents
20 is What Percent of 36: A Comprehensive Guide to Percentage Calculations
This article delves into the question, "20 is what percent of 36?", providing a thorough explanation of the calculation process and exploring related percentage concepts. We'll cover the fundamental formula, demonstrate various solution methods, and examine practical applications of percentage calculations in everyday life. Understanding percentages is crucial for various aspects of life, from budgeting and finance to understanding statistics and data analysis. This comprehensive guide will equip you with the knowledge and skills to confidently tackle any percentage problem.
What are Percentages?
Percentages are a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred," and the symbol "%" represents this division. Percentages are used extensively to represent proportions, ratios, and changes in values. For instance, a 10% discount means you save 10 out of every 100 units of currency. Understanding percentages is crucial for interpreting data, making comparisons, and solving real-world problems.
Calculating "20 is What Percent of 36?"
The core problem, "20 is what percent of 36?", translates into a simple mathematical equation. We can represent the unknown percentage as 'x'. The equation then becomes:
20 = x% * 36
To solve for 'x', we need to isolate it on one side of the equation. Here's a step-by-step process:
-
Convert the percentage to a decimal: To work with percentages in equations, we convert them to decimals by dividing by 100. So, x% becomes x/100.
-
Rewrite the equation: Substituting the decimal equivalent, our equation becomes:
20 = (x/100) * 36
-
Solve for x: To isolate 'x', we can follow these steps:
- Multiply both sides of the equation by 100: 2000 = 36x
- Divide both sides by 36: x = 2000/36
- Simplify the fraction: x ≈ 55.56
Therefore, 20 is approximately 55.56% of 36.
Alternative Methods for Calculating Percentages
While the above method is straightforward, several alternative approaches can be used to solve percentage problems. These methods provide flexibility and can be beneficial depending on the complexity of the problem.
-
Using Proportions: Percentages can be expressed as ratios. We can set up a proportion:
20/36 = x/100
Cross-multiplying gives: 36x = 2000
Solving for x: x ≈ 55.56
-
Using a Calculator: Most calculators have a percentage function. Simply enter 20 ÷ 36 and then multiply by 100 to obtain the percentage.
Understanding the Result: 55.56%
The result, approximately 55.56%, signifies that 20 represents a little more than half of 36. This percentage indicates the proportional relationship between 20 and 36, showing how much of 36 is represented by 20.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various real-world scenarios. Understanding them is vital for navigating everyday life effectively. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes is vital for tracking financial performance. For example, if your investment grows by 15%, you know its value increased by 15% of its initial value.
-
Shopping: Discounts are often expressed as percentages. For instance, a 20% discount on a $100 item means you save $20. Calculating the final price after discounts requires understanding percentage reductions.
-
Statistics and Data Analysis: Percentages are fundamental to representing data in charts, graphs, and tables. They are frequently used to express probabilities, proportions, and changes over time in data analysis. For example, analyzing survey data often involves presenting the results as percentages to easily compare different groups.
-
Science and Engineering: Percentage error, efficiency, and concentration are commonly expressed as percentages in scientific and engineering contexts.
-
Everyday Life: Percentage calculations appear in various everyday tasks, like calculating tips in restaurants, figuring out sale prices, and understanding nutritional information on food labels.
Advanced Percentage Concepts
Beyond basic percentage calculations, understanding more advanced concepts can deepen your proficiency. These include:
-
Percentage Increase/Decrease: Calculating the percentage change between two values, whether an increase or decrease, involves determining the difference between the values, dividing this difference by the original value, and multiplying by 100.
-
Compound Interest: Compound interest is interest calculated on both the principal amount and accumulated interest. This leads to exponential growth, and understanding how to calculate compound interest is crucial for long-term financial planning.
-
Percentage Points: Percentage points represent the arithmetic difference between two percentages. It's not the same as a percentage change. For instance, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
-
Percentage of a Percentage: Calculating a percentage of a percentage involves multiplying the two percentages (converted to decimals) to get the final percentage. For example, 20% of 50% is 0.20 * 0.50 = 0.10 or 10%.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Work through various problems, gradually increasing their complexity.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of percentages, ratios, and proportions.
-
Use Visual Aids: Diagrams, charts, and graphs can help visualize percentages and improve your understanding.
-
Utilize Online Resources: Numerous online resources, including calculators, tutorials, and practice problems, can aid your learning.
Conclusion
In conclusion, 20 is approximately 55.56% of 36. This seemingly simple calculation underlies a vast range of applications in various fields. Mastering percentage calculations is a valuable skill that enhances your ability to interpret data, solve problems, and navigate everyday life more effectively. By understanding the fundamental concepts and applying the different calculation methods, you'll be well-equipped to tackle percentage problems with confidence and efficiency. Remember to practice regularly and explore the advanced concepts to further expand your knowledge and expertise in this essential mathematical area.
Latest Posts
Latest Posts
-
How To Tell A Chemical Reaction Has Occurred
Apr 19, 2025
-
How Much Is 23 Degrees Celsius In Fahrenheit
Apr 19, 2025
-
How Much Is 160 Celsius In Fahrenheit
Apr 19, 2025
-
How Many Pounds In 2000 Grams
Apr 19, 2025
-
What Percent Is 14 Out Of 20
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.