20 Is What Percent Of 4
Kalali
Apr 23, 2025 · 5 min read
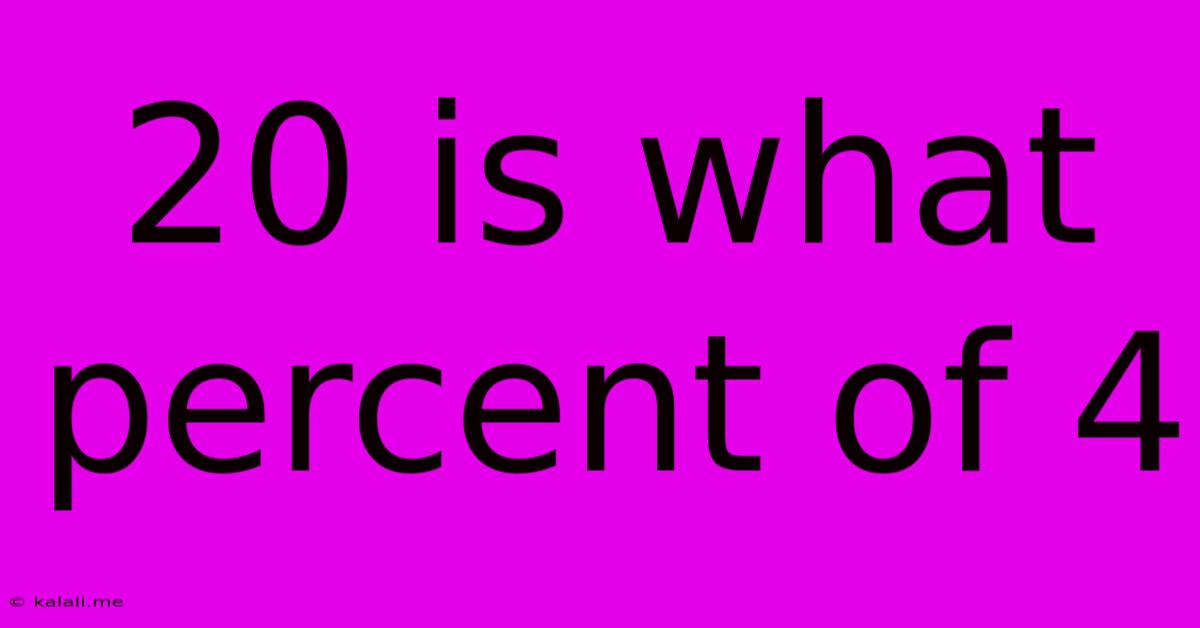
Table of Contents
20 is What Percent of 4? Understanding Percentages and Their Applications
This seemingly simple question, "20 is what percent of 4?", opens the door to a vast world of mathematical concepts and practical applications. While the answer might seem immediately obvious to some, understanding the underlying principles behind percentage calculations is crucial for various aspects of life, from everyday finances to advanced statistical analysis. This article delves deep into the solution, explores different methods of calculation, and illuminates the broader significance of percentages in our world.
Meta Description: Discover how to calculate percentages, understand the concept of "20 is what percent of 4," and explore its practical applications in everyday life and various fields. Learn multiple methods and master percentage calculations.
Understanding the Fundamentals of Percentages
A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are a common way to express proportions, ratios, and rates of change. They provide a standardized and easily understandable way to compare different quantities.
Method 1: Using the Basic Percentage Formula
The most straightforward approach to solving "20 is what percent of 4?" involves using the fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 20
- Whole: 4
Plugging these values into the formula, we get:
(20 / 4) * 100% = 500%
Therefore, 20 is 500% of 4.
Method 2: Solving for the Unknown Percentage
We can also approach the problem by setting up an equation and solving for the unknown percentage (let's represent it as 'x'):
x% of 4 = 20
This can be rewritten as:
(x/100) * 4 = 20
Now, we solve for x:
- Multiply both sides by 100: 4x = 2000
- Divide both sides by 4: x = 500
Thus, again, we find that x = 500%, confirming that 20 is 500% of 4. This method is particularly useful when dealing with more complex percentage problems where the part or the whole is unknown.
Method 3: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion as follows:
20/4 = x/100
This proportion states that the ratio of 20 to 4 is equal to the ratio of x (the unknown percentage) to 100. To solve for x, we cross-multiply:
20 * 100 = 4 * x
2000 = 4x
x = 500
Once again, we arrive at the answer: 20 is 500% of 4. This method highlights the relationship between ratios and percentages, demonstrating their interconnectedness.
Why the Result is Greater Than 100%
It's important to note that a percentage greater than 100% is perfectly valid and simply indicates that the "part" is larger than the "whole." In this case, 20 is more than four times larger than 4, hence the result exceeding 100%. This scenario frequently arises in various contexts, such as comparing growth rates, increases in value, or analyzing data where the final value surpasses the initial value.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations. Here are a few examples:
- Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all rely heavily on percentage calculations. For instance, determining the interest earned on a savings account or the total cost of an item after sales tax involves direct application of percentage principles.
- Business: Businesses use percentages extensively for analyzing sales figures, market share, profit and loss statements, and calculating growth rates. Understanding these percentages is crucial for strategic decision-making and business planning.
- Science and Statistics: Percentages are fundamental to statistical analysis, representing proportions within data sets, expressing probabilities, and calculating error margins. Scientific experiments often involve percentage calculations for comparing results and drawing conclusions.
- Everyday Life: We encounter percentages daily in various contexts, such as calculating tips in restaurants, understanding sales discounts, interpreting survey results, and assessing nutritional information on food labels.
Advanced Percentage Calculations and Problem Solving
While the problem "20 is what percent of 4?" provides a basic introduction to percentage calculations, more complex scenarios require a deeper understanding and application of algebraic principles.
For example, consider the problem: "If a product's price increases by 15% from $50 to $57.50, and then decreases by 10% of the new price, what is the final price?" This requires a step-by-step approach incorporating multiple percentage calculations.
Such problems demand a clear understanding of the underlying principles, the ability to translate word problems into mathematical equations, and the skill to solve these equations systematically. Mastering these techniques is valuable for tackling intricate percentage-related issues encountered in various fields.
Expanding Knowledge: Proportions, Ratios, and Rates
Percentages are closely linked to proportions, ratios, and rates. Understanding these concepts enriches the comprehension of percentages and enhances problem-solving capabilities.
A ratio compares two quantities, while a proportion states that two ratios are equal. A rate compares two quantities with different units, such as speed (miles per hour) or price per unit. Mastering these concepts strengthens your ability to work with percentages in more complex situations.
Conclusion: The Power of Percentage Understanding
The seemingly simple question, "20 is what percent of 4?", serves as a gateway to understanding the power and versatility of percentage calculations. From everyday finances to advanced scientific analysis, percentages are an indispensable tool. By mastering different calculation methods and understanding their broader implications, we equip ourselves with valuable skills applicable across numerous aspects of life, enhancing both problem-solving capabilities and our comprehension of the world around us. The ability to confidently calculate and interpret percentages is a key component of numerical literacy, a skill increasingly important in our data-driven world. Continue practicing various percentage problems to build fluency and confidence in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Signs That A Chemical Reaction Has Occurred
May 09, 2025
-
What Is 2 75 As A Fraction
May 09, 2025
-
Cuanto Es 164 Cm En Pies
May 09, 2025
-
Atomic Mass And Atomic Number Worksheet
May 09, 2025
-
Least Common Multiple Of 8 And 18
May 09, 2025
Related Post
Thank you for visiting our website which covers about 20 Is What Percent Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.