20 Of 80 Is What Number
Kalali
Apr 16, 2025 · 5 min read
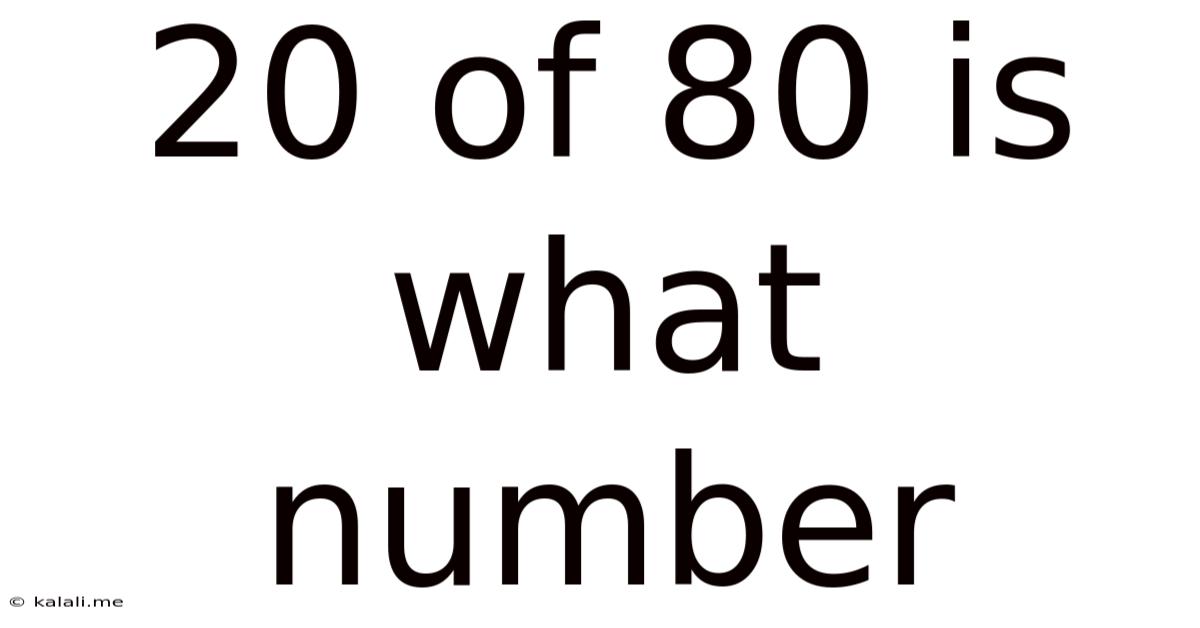
Table of Contents
20 out of 80: Understanding Percentages, Fractions, and Ratios
This seemingly simple question, "20 out of 80 is what number?", opens the door to a deeper understanding of fundamental mathematical concepts like percentages, fractions, and ratios. It's more than just finding a single numerical answer; it's about grasping the relationships between different ways of expressing proportions. This article will explore various methods to solve this problem, explaining the underlying principles and providing practical applications for everyday life. We'll also delve into the importance of these concepts in various fields, showcasing their relevance beyond simple arithmetic.
Meta Description: Discover multiple ways to solve "20 out of 80 is what number?" Learn about percentages, fractions, ratios, and their applications in everyday life and various fields. This comprehensive guide explains the underlying mathematical principles and offers practical examples.
Understanding the Problem: Parts and Wholes
The core of the problem lies in understanding the relationship between a part (20) and a whole (80). We want to determine what proportion 20 represents of the total 80. This proportion can be expressed in several ways, each with its own advantages and applications.
Method 1: Using Fractions
The most straightforward approach is to express the relationship as a fraction. The fraction representing "20 out of 80" is written as 20/80. This fraction can then be simplified by finding the greatest common divisor (GCD) of the numerator (20) and the denominator (80). The GCD of 20 and 80 is 20. Dividing both the numerator and the denominator by 20 simplifies the fraction to 1/4.
Therefore, 20 out of 80 is equivalent to 1/4. This fraction represents one part out of four equal parts.
Method 2: Calculating the Percentage
Percentages provide a standardized way to compare proportions. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In our case:
(20 / 80) * 100% = 0.25 * 100% = 25%
Therefore, 20 out of 80 is 25%. This means that 20 represents 25% of the total 80. Percentages are widely used in various contexts, from calculating discounts and sales tax to expressing statistical data and financial performance.
Method 3: Using Ratios
Ratios express the relationship between two quantities. The ratio of 20 to 80 can be written as 20:80. Similar to fractions, this ratio can be simplified by dividing both numbers by their GCD (20), resulting in a simplified ratio of 1:4.
The ratio 1:4 indicates that for every one part, there are four parts in total. Ratios are frequently used in various fields, including cooking, map scaling, and comparing quantities in science and engineering.
Practical Applications: Real-world Examples
The concepts of fractions, percentages, and ratios are not merely abstract mathematical ideas; they are essential tools for navigating everyday situations. Here are some real-world applications:
- Shopping: Calculating discounts, sales tax, and comparing prices. If a shirt is discounted by 25%, and the original price was $80, you can easily calculate the discount amount using the percentage method.
- Cooking: Following recipes and adjusting ingredient quantities. If a recipe calls for a 1:2 ratio of sugar to flour, you can easily scale the recipe up or down.
- Finance: Calculating interest rates, loan repayments, and investment returns. Percentages are crucial for understanding financial gains and losses.
- Data Analysis: Interpreting statistical data and representing proportions in charts and graphs. For example, representing the percentage of students who passed an exam.
- Construction and Engineering: Measuring quantities, calculating material requirements, and scaling blueprints. Ratios and fractions are vital for accurate measurements and calculations.
- Science: Expressing concentrations of solutions, determining proportions of elements in compounds, and analyzing experimental results. Ratios and percentages are used extensively to represent data in a concise manner.
Expanding the Concept: Beyond Simple Arithmetic
While the problem "20 out of 80 is what number?" might seem elementary, it serves as a stepping stone to more complex mathematical concepts. Here are some areas where a deeper understanding of proportions becomes crucial:
- Algebra: Solving equations involving proportions. The same principles applied here can be extended to solving algebraic equations involving variables.
- Geometry: Calculating areas, volumes, and ratios of similar figures. Proportions are fundamental in geometry for understanding similar shapes and scaling.
- Probability and Statistics: Calculating probabilities and analyzing statistical data. Percentages are widely used to represent probabilities and frequency distributions.
- Calculus: Understanding rates of change and derivatives. The concept of proportions is essential for understanding the fundamental principles of calculus.
Dealing with More Complex Proportions
Let's consider a slightly more challenging scenario. What if we had a problem like "35 out of 175 is what number?" The same methods apply, but the calculations might be slightly more involved.
- Fraction: 35/175 simplifies to 1/5.
- Percentage: (35/175) * 100% = 20%
- Ratio: 35:175 simplifies to 1:5
This demonstrates the versatility and applicability of these methods across a range of numerical values. Regardless of the numbers involved, the underlying principles of determining the proportion of a part to a whole remain consistent.
Importance of Understanding Proportions in Different Fields
The ability to accurately calculate and interpret proportions is invaluable across numerous professional fields. Consider the following examples:
- Marketing: Analyzing website traffic, conversion rates, and customer engagement metrics. Understanding percentages and ratios is crucial for evaluating marketing campaigns.
- Healthcare: Calculating medication dosages, interpreting medical test results, and analyzing epidemiological data. Accuracy in proportions is paramount in healthcare.
- Education: Assessing student performance, analyzing test scores, and evaluating curriculum effectiveness. Percentages and ratios are essential for educational assessment.
- Environmental Science: Analyzing pollution levels, monitoring biodiversity, and predicting environmental changes. Proportions are crucial for expressing environmental data and modeling environmental changes.
Conclusion: Mastering Proportions for Success
The seemingly simple question, "20 out of 80 is what number?", provides a valuable entry point into the broader world of mathematical proportions. By mastering the techniques of calculating percentages, fractions, and ratios, you equip yourself with essential tools applicable in various aspects of life, from everyday tasks to specialized professions. Understanding these concepts enhances your analytical skills and allows you to confidently interpret and utilize numerical information in a variety of contexts. The ability to easily switch between these different representations of proportion not only simplifies calculations but also improves comprehension and problem-solving abilities. So, next time you encounter a proportion problem, remember the fundamental principles and the diverse ways you can approach the solution.
Latest Posts
Latest Posts
-
How Many Seconds Is In 3 Hours
May 09, 2025
-
Cuanto Es 32 Onzas En Mililitros
May 09, 2025
-
What Is The Main Effect Of Overpopulation On Animals
May 09, 2025
-
59 Out Of 75 As A Percentage
May 09, 2025
-
What Is The Charge Of K
May 09, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 80 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.