21 Is What Percent Of 25
Kalali
Apr 11, 2025 · 5 min read
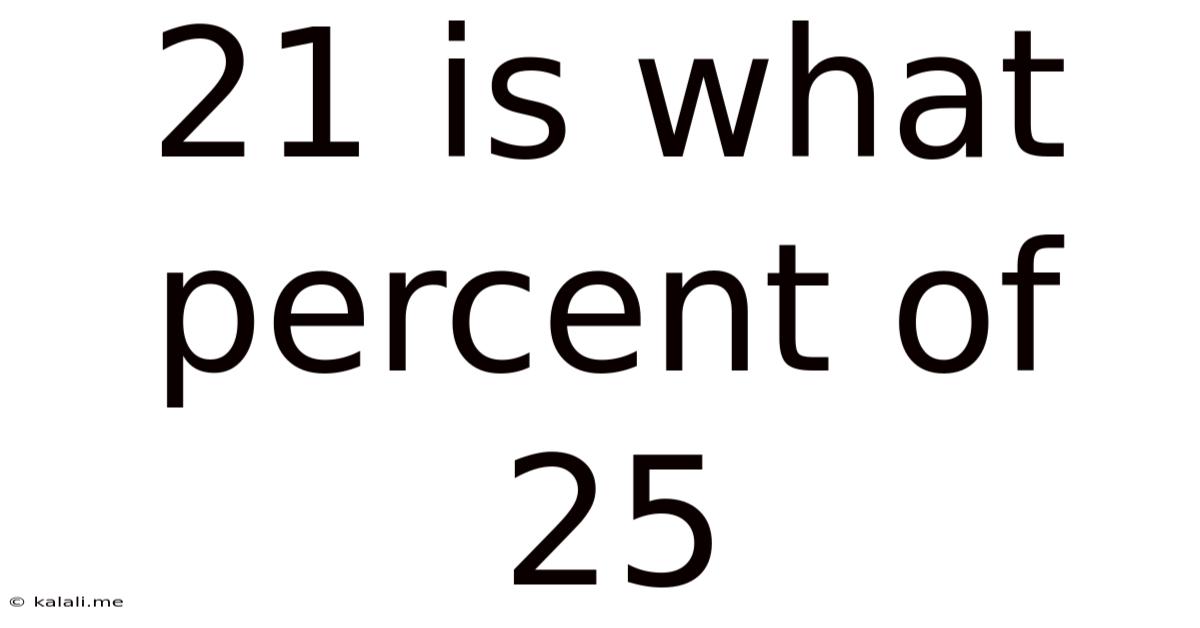
Table of Contents
21 is What Percent of 25? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "21 is what percent of 25?", opens the door to a fascinating exploration of percentages, their practical applications, and how to solve percentage problems efficiently and accurately. Understanding percentages is crucial in numerous fields, from finance and business to everyday life calculations. This article will not only answer the initial question but will also equip you with the knowledge and techniques to tackle similar problems confidently. We'll delve into various methods, explore real-world examples, and uncover the underlying mathematical principles.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide explains how to determine what percent 21 is of 25, covering multiple methods and real-world applications of percentage calculations. Master percentage problems and improve your mathematical skills.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." So, 25% is equivalent to 25/100, or 0.25 as a decimal. This fundamental concept allows us to represent parts of a whole in a standardized and easily comparable way. Understanding this relationship is vital for solving any percentage problem.
Method 1: The Direct Formula Approach
The most straightforward method to determine what percentage 21 represents of 25 is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 21
- Whole: 25
Plugging these values into the formula:
(21 / 25) * 100% = 84%
Therefore, 21 is 84% of 25.
Method 2: Using Decimal Equivalents
This method involves converting the fraction to a decimal and then multiplying by 100%. Let's follow the steps:
-
Convert the fraction: Divide the part (21) by the whole (25): 21 / 25 = 0.84
-
Convert to percentage: Multiply the decimal by 100%: 0.84 * 100% = 84%
This method provides the same result: 21 is 84% of 25.
Method 3: Proportion Method
The proportion method utilizes the concept of equivalent ratios. We set up a proportion to solve for the unknown percentage (x):
21/25 = x/100
To solve for x, we cross-multiply:
21 * 100 = 25 * x
2100 = 25x
x = 2100 / 25
x = 84
Therefore, x = 84%, confirming that 21 is 84% of 25.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is essential in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding compound interest, for instance, requires a solid grasp of percentage growth. Determining the percentage change in a stock price or the interest accrued on a loan are critical financial calculations.
-
Business: Analyzing sales figures, market share, profit margins, and cost of goods sold all involve calculating percentages. Businesses use percentages to track key performance indicators (KPIs), make informed decisions, and project future growth. Understanding percentage change in sales from one quarter to the next, for example, is essential for business planning.
-
Retail: Discounts are often expressed as percentages. Calculating the final price after a 20% discount or determining the original price before a sale requires percentage calculations. Similarly, sales tax is typically added as a percentage of the purchase price.
-
Science: Many scientific calculations involve percentages. For example, calculating the percentage of a particular element in a compound, expressing experimental error as a percentage, or determining the percentage of a population with a certain characteristic. Data analysis frequently involves expressing results as percentages.
-
Everyday Life: We encounter percentages daily: tipping at a restaurant, calculating the percentage of a task completed, understanding nutritional information (percentage of daily value), or interpreting statistics presented in news reports. Understanding percentages enhances our ability to interpret information effectively and make informed decisions.
Beyond the Basics: More Complex Percentage Problems
While the question "21 is what percent of 25?" is relatively straightforward, many percentage problems are more complex. Let's explore some variations:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example: "21 is 84% of what number?" This would require rearranging the percentage formula to solve for the whole.
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example: "What is 84% of 25?"
-
Percentage Increase/Decrease: These problems involve calculating the percentage change between two values. For example: "A price increased from $25 to $35. What is the percentage increase?" This requires calculating the difference, dividing it by the original value, and multiplying by 100%.
-
Compound Interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. This requires repeated percentage calculations over time and demonstrates the power of exponential growth.
Tips for Solving Percentage Problems
-
Understand the language: Carefully read the problem to identify the known and unknown values.
-
Use the correct formula: Choose the appropriate formula based on the information provided.
-
Show your work: Writing down each step helps prevent errors and allows you to review your work.
-
Check your answer: Make sure your answer is reasonable and makes sense in the context of the problem.
-
Practice regularly: Consistent practice is key to mastering percentage calculations.
Conclusion: Mastering Percentages for a Better Understanding of the World
The ability to confidently calculate and understand percentages is a valuable skill applicable across various disciplines and everyday life. This article has shown how to determine that 21 is 84% of 25 using multiple methods, highlighting the importance of understanding the fundamental principles and applying them to solve diverse percentage-related problems. From complex financial models to simple everyday calculations, a strong grasp of percentages empowers you to navigate the quantitative aspects of the world with greater ease and accuracy. By understanding the underlying mathematical concepts and practicing regularly, you can develop the skills needed to approach and solve a wide range of percentage problems with confidence.
Latest Posts
Latest Posts
-
Does Liquid Have A Definite Volume
Apr 18, 2025
-
How Many Cups In 64 Ounces Of Water
Apr 18, 2025
-
What Percentage Is 15 Out Of 20
Apr 18, 2025
-
How Many Litres In A 5 Gallon Bucket
Apr 18, 2025
-
Does Gold Set Off A Metal Detector
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 21 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.