21 Out Of 28 As A Percentage
Kalali
Apr 23, 2025 · 5 min read
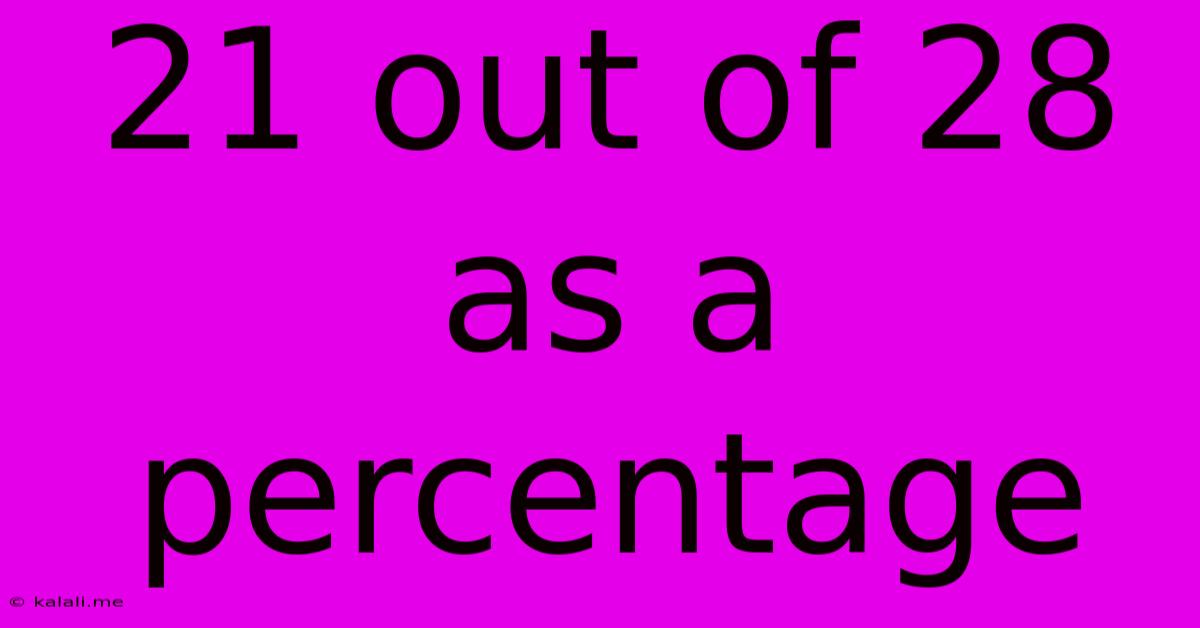
Table of Contents
21 out of 28 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and excelling in various academic and professional contexts. This article will delve into the specifics of calculating "21 out of 28 as a percentage," providing a step-by-step guide, exploring related concepts, and offering practical applications. Understanding this specific calculation will empower you to confidently tackle similar percentage problems.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Percentages are widely used because they provide a standardized way to compare proportions and make sense of data regardless of the initial size of the whole.
Calculating 21 out of 28 as a Percentage: The Step-by-Step Method
To calculate 21 out of 28 as a percentage, we follow these simple steps:
-
Form a Fraction: Express the given numbers as a fraction. In this case, 21 is the part and 28 is the whole. Therefore, the fraction is 21/28.
-
Convert the Fraction to a Decimal: Divide the numerator (21) by the denominator (28). 21 ÷ 28 = 0.75
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.75 x 100 = 75%.
Therefore, 21 out of 28 is equal to 75%.
Understanding the Concept of Ratios and Proportions
The calculation above utilizes the concept of ratios and proportions. A ratio is a comparison of two numbers, often expressed as a fraction. A proportion is a statement that two ratios are equal. In our example, the ratio 21:28 is proportional to the ratio 75:100 (or 75%). Understanding these concepts is vital for comprehending percentage calculations and their applications in various fields.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in a multitude of situations, including:
-
Academic Assessments: Calculating grades, test scores, and assignment marks often involves determining percentages. For example, if you scored 21 out of 28 on a quiz, your score is 75%.
-
Financial Calculations: Percentages are fundamental in finance, used for calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage change is crucial for analyzing financial trends.
-
Data Analysis and Statistics: Percentages are used to represent data in charts and graphs, making it easier to visualize and interpret trends and patterns. For instance, market research often uses percentages to represent customer preferences or market share.
-
Everyday Life: We encounter percentages daily, from sale discounts in stores to calculating tips in restaurants. Understanding percentages helps us make informed decisions and manage our finances effectively.
-
Scientific Research: Percentages are used extensively in scientific research to represent proportions, probabilities, and error margins.
Beyond the Basics: More Complex Percentage Calculations
While calculating "21 out of 28 as a percentage" is a straightforward example, many real-world scenarios involve more complex percentage calculations. Let's explore some of them:
-
Calculating Percentage Increase or Decrease: This involves finding the percentage change between two numbers. For example, if a product's price increased from $28 to $35, the percentage increase is calculated as follows:
- Find the difference: $35 - $28 = $7
- Divide the difference by the original value: $7 / $28 = 0.25
- Multiply by 100 to express as a percentage: 0.25 x 100 = 25%
The price increased by 25%.
-
Calculating Percentage of a Number: This involves finding a specific percentage of a given number. For example, to find 75% of 120, you would multiply 120 by 0.75: 120 x 0.75 = 90.
-
Finding the Original Value after a Percentage Change: This involves working backward from a percentage change to find the original value. For example, if a price increased by 20% to reach $30, the original price can be calculated as follows:
- Express the percentage increase as a decimal: 20% = 0.20
- Add 1 to the decimal: 1 + 0.20 = 1.20
- Divide the final value by the result: $30 / 1.20 = $25
The original price was $25.
Using Technology for Percentage Calculations
While manual calculations are valuable for understanding the underlying concepts, technology can significantly simplify the process. Many calculators and spreadsheet programs (like Microsoft Excel or Google Sheets) have built-in functions for calculating percentages, making complex calculations quick and efficient. Learning to utilize these tools can save time and improve accuracy.
Common Mistakes to Avoid When Calculating Percentages
Several common mistakes can lead to inaccurate percentage calculations. Be mindful of these:
-
Incorrect Fraction Formation: Ensure the correct number represents the "part" and the other the "whole" when forming the initial fraction.
-
Order of Operations: When dealing with multiple operations, follow the order of operations (PEMDAS/BODMAS) to avoid errors.
-
Decimal Place Errors: Pay close attention to decimal places during calculations to maintain accuracy.
-
Misinterpreting Percentage Changes: Clearly understand whether you're calculating a percentage increase, decrease, or a simple percentage of a number.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a highly valuable skill with broad applications. Understanding the fundamental principles, as illustrated by the calculation of "21 out of 28 as a percentage," along with the various practical applications and potential pitfalls, empowers you to confidently tackle a wide range of percentage problems in academic, professional, and personal settings. By mastering these concepts, you can enhance your analytical skills and make more informed decisions in various aspects of life. Remember to practice regularly and utilize available tools to improve your proficiency and accuracy. This will not only improve your understanding of mathematics but will also make you a more effective problem-solver in many areas of your life.
Latest Posts
Latest Posts
-
Did Chester Wear A Brace On Gunsmoke
Jul 15, 2025
-
How Many Mikes Hard To Get Drunk
Jul 15, 2025
-
How Many Liters Has In Half Gallon
Jul 15, 2025
-
How Much Is Half Of A Mile
Jul 15, 2025
-
What Letter Is Halfway Through The Alphabet
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about 21 Out Of 28 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.