21 Out Of 35 As A Percentage
Kalali
Apr 23, 2025 · 5 min read
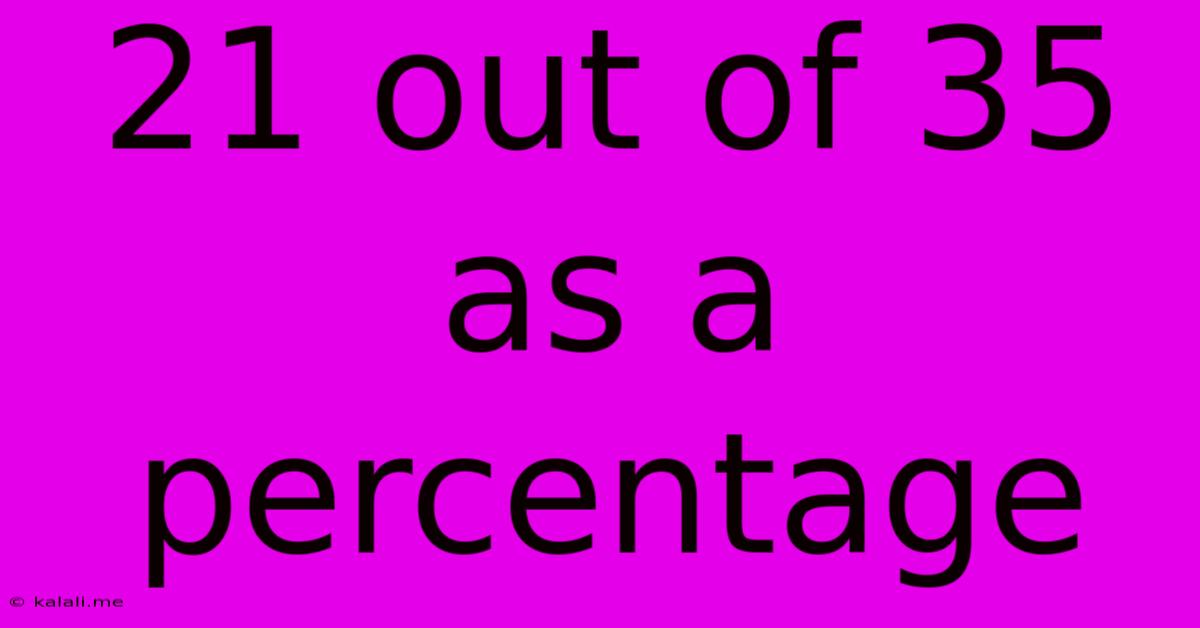
Table of Contents
21 out of 35 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific analyses and financial modeling. Understanding how to express a ratio as a percentage is crucial for interpreting data, making informed decisions, and communicating results effectively. This article delves into the calculation of 21 out of 35 as a percentage, providing a step-by-step guide, exploring different calculation methods, and offering practical examples to solidify your understanding. We'll also look at the broader context of percentage calculations and their significance.
Meta Description: Learn how to calculate 21 out of 35 as a percentage. This comprehensive guide provides step-by-step instructions, explores different methods, and offers practical examples to master percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 21 out of 35 represents a part of a whole, and converting this ratio to a percentage allows us to express this part in terms of 100. This standardized representation facilitates easy comparison and interpretation of proportions. For example, understanding that 60% of students passed an exam is immediately more meaningful than knowing that 18 out of 30 students passed.
Method 1: Using the Basic Formula
The most straightforward method to calculate 21 out of 35 as a percentage involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 21
- Whole: 35
Substituting these values into the formula:
(21 / 35) * 100% = 60%
Therefore, 21 out of 35 is equal to 60%.
Method 2: Simplifying the Fraction
Before applying the percentage formula, simplifying the fraction can make the calculation easier. The fraction 21/35 can be simplified by finding the greatest common divisor (GCD) of 21 and 35, which is 7. Dividing both the numerator and denominator by 7:
21 ÷ 7 = 3 35 ÷ 7 = 5
This simplifies the fraction to 3/5. Now, applying the percentage formula:
(3 / 5) * 100% = 60%
This confirms that 21 out of 35 is indeed 60%. Simplifying the fraction often makes manual calculations simpler, especially when dealing with larger numbers.
Method 3: Using a Calculator
Calculators provide a quick and efficient way to calculate percentages. Simply divide the part (21) by the whole (35), and then multiply the result by 100. Most calculators have a percentage function (%) that simplifies this process even further.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples showcasing the practical application of converting 21 out of 35 to 60%:
- Academic Performance: If a student answered 21 questions correctly out of 35 on a test, their score is 60%. This provides a clear understanding of their performance relative to the total number of questions.
- Sales and Marketing: If a salesperson achieved 21 sales out of a target of 35, their success rate is 60%. This metric helps in evaluating sales performance and identifying areas for improvement.
- Project Management: If 21 tasks out of a total of 35 planned tasks are completed, 60% of the project is finished. This allows for better project tracking and progress monitoring.
- Financial Analysis: If a company invested in 35 projects and 21 were successful, its success rate is 60%. This helps in assessing investment strategies and resource allocation.
- Data Analysis: In various data analysis tasks, expressing a ratio as a percentage often simplifies the interpretation and comparison of different datasets.
Beyond the Basics: Working with Percentages
While calculating 21 out of 35 as a percentage is straightforward, understanding percentages extends beyond simple calculations. Here are some related concepts and applications:
- Percentage Increase/Decrease: Calculating the percentage change between two values is a common application. For example, if sales increased from 35 units to 56 units, the percentage increase would be calculated as: ((56-35)/35) * 100% = 60%.
- Percentage Points: Percentage points represent the arithmetic difference between two percentages, not the percentage change. For example, if interest rates increased from 5% to 11%, the increase is 6 percentage points, not a 120% increase.
- Compounding Percentages: In finance and other areas, percentages can compound over time. For instance, if an investment grows by 10% each year for three years, the final value will be greater than simply adding 30% to the initial value due to the compounding effect.
- Weighted Averages: When dealing with multiple percentages with different weights or significances, weighted averages are used to calculate an overall percentage.
Advanced Percentage Calculations and Applications
Percentage calculations play a vital role in more advanced applications including:
- Statistical Analysis: Percentages are used extensively in statistical analysis to represent proportions, probabilities, and confidence intervals. For example, confidence intervals are often expressed as percentages (e.g., 95% confidence interval).
- Financial Modeling: In financial modeling, percentages are used to project future growth, discount cash flows, and assess investment risk. For instance, discounted cash flow analysis heavily relies on percentage-based discount rates.
- Scientific Research: Scientific research often involves expressing data as percentages to represent proportions or rates of change. This is crucial for comparing results across different experiments or groups.
Troubleshooting Common Mistakes in Percentage Calculations
Several common mistakes can occur when calculating percentages. Here are some to watch out for:
- Incorrect Order of Operations: Always remember the order of operations (PEMDAS/BODMAS). Division should be performed before multiplication.
- Confusing Percentage Points and Percentage Change: Remember the difference between percentage points and percentage change.
- Rounding Errors: Rounding numbers prematurely during calculations can lead to inaccuracies in the final result. It's best to use the full precision of your calculator until the final answer.
- Incorrect Interpretation: Misinterpreting the percentage result can lead to wrong conclusions. Always ensure you understand the context and meaning of the calculated percentage.
Conclusion: Mastering Percentage Calculations
Calculating 21 out of 35 as a percentage, resulting in 60%, is a fundamental skill with far-reaching applications. This guide has provided multiple methods for calculating percentages, explored their practical uses across various fields, and highlighted common pitfalls. By understanding these concepts and techniques, you'll be well-equipped to handle percentage calculations with confidence and accuracy in all your endeavors. Remember to practice regularly, and as you progress, explore more advanced applications like compound interest calculations and statistical analysis to enhance your numerical literacy.
Latest Posts
Latest Posts
-
133 Cm To Inches And Feet
May 09, 2025
-
What Are The Factors Of M2 12m 20
May 09, 2025
-
How Much Is 6 Quarts In Liters
May 09, 2025
-
Least Common Multiple Of 6 And 15
May 09, 2025
-
Which Best Describes The Diameter Of A Circle
May 09, 2025
Related Post
Thank you for visiting our website which covers about 21 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.