22 15 As A Mixed Number
Kalali
Apr 19, 2025 · 5 min read
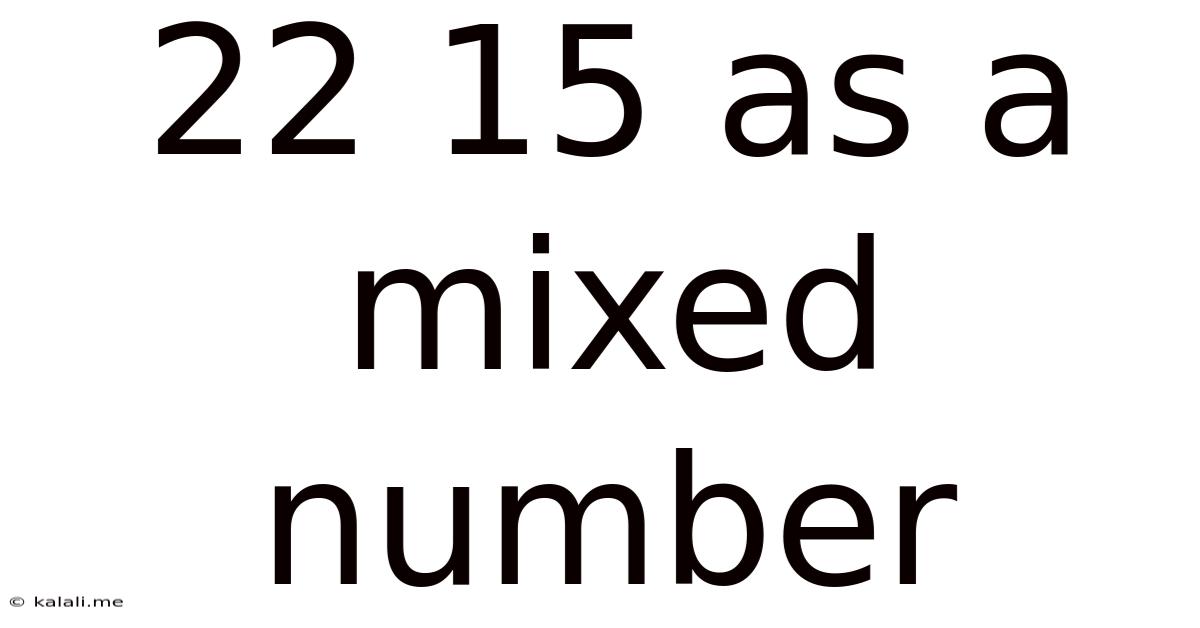
Table of Contents
Understanding 22/15 as a Mixed Number: A Comprehensive Guide
Meta Description: Learn how to convert the improper fraction 22/15 into a mixed number. This comprehensive guide explains the process step-by-step, provides examples, and explores related concepts like simplifying fractions and converting between improper and mixed numbers. We'll also cover practical applications and troubleshooting common mistakes.
Converting improper fractions to mixed numbers is a fundamental skill in mathematics, crucial for understanding fractions and their applications in various fields. This article provides a thorough explanation of how to convert the improper fraction 22/15 into a mixed number, covering the process, related concepts, and practical applications. We'll explore the underlying principles and address potential challenges, ensuring a complete understanding of this important mathematical concept.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). In our case, 22/15 is an improper fraction because 22 (numerator) is greater than 15 (denominator). Improper fractions represent a value greater than or equal to one. Other examples include 7/4, 11/3, and 25/5.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator (e.g., 1/2, 3/4, 7/8). Mixed numbers provide a more intuitive way to represent values greater than one. For instance, 1 ½ represents one whole and one-half.
Converting 22/15 to a Mixed Number: A Step-by-Step Guide
The conversion of 22/15 to a mixed number involves dividing the numerator by the denominator. Here's how:
-
Divide the Numerator by the Denominator: Divide 22 by 15.
22 ÷ 15 = 1 with a remainder of 7
-
Identify the Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
-
Identify the Numerator of the Fraction: The remainder from the division becomes the numerator of the fractional part of the mixed number. The remainder is 7.
-
Retain the Original Denominator: The denominator of the fraction in the mixed number remains the same as the original denominator. The denominator remains 15.
-
Combine the Whole Number and the Fraction: Combine the whole number and the fraction to form the mixed number.
Therefore, 22/15 as a mixed number is 1 7/15.
Visualizing the Conversion
Imagine you have 22 pieces of pizza, and each pizza is cut into 15 slices. You can assemble 1 whole pizza (15 slices) and have 7 slices remaining. This remaining 7 slices represent 7/15 of a pizza. Thus, you have 1 whole pizza and 7/15 of another, which is represented by the mixed number 1 7/15.
Simplifying Fractions: An Important Consideration
Before or after converting to a mixed number, it's always good practice to check if the fraction can be simplified. A fraction is simplified when the numerator and denominator share no common factors other than 1. In our example, 7 and 15 have no common factors other than 1, so 7/15 is already in its simplest form. However, if the fraction had been, say, 24/18, we would simplify it to 4/3 before converting to a mixed number.
Converting Mixed Numbers Back to Improper Fractions
It's useful to understand the reverse process as well. To convert a mixed number back to an improper fraction:
-
Multiply the whole number by the denominator: For 1 7/15, multiply 1 (whole number) by 15 (denominator) = 15.
-
Add the numerator: Add the result from step 1 to the numerator: 15 + 7 = 22.
-
Keep the denominator the same: The denominator remains 15.
-
Form the improper fraction: Combine the results to form the improper fraction: 22/15.
Practical Applications of Improper Fractions and Mixed Numbers
Understanding improper fractions and mixed numbers is essential in various real-life situations:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Converting between improper fractions and mixed numbers helps in accurately measuring ingredients.
-
Construction and Engineering: Precise measurements are critical in these fields. Fractions are frequently used to represent dimensions and quantities.
-
Finance and Accounting: Calculations involving money often involve fractions and mixed numbers, especially when dealing with percentages and interest rates.
-
Data Analysis: In statistical analysis, representing data using fractions and mixed numbers can be essential for understanding proportions and ratios.
Common Mistakes to Avoid
-
Incorrect Division: Ensuring accurate division of the numerator by the denominator is crucial. A simple calculation error can lead to an incorrect mixed number.
-
Forgetting the Remainder: The remainder is a vital part of the process. Omitting it will result in an incomplete and inaccurate mixed number.
-
Incorrect Simplification: Always check if the fractional part of the mixed number can be simplified. Leaving a fraction unsimplified can make the answer less clear and efficient.
-
Confusing Numerator and Denominator: Pay close attention to which number is the numerator and which is the denominator. Confusion can lead to incorrect calculations.
Further Exploration: Working with Larger Numbers
The principles for converting improper fractions to mixed numbers remain the same even with larger numbers. For example, consider the fraction 157/25:
-
Divide: 157 ÷ 25 = 6 with a remainder of 7.
-
Whole number: The whole number is 6.
-
Numerator: The remainder is 7.
-
Denominator: The denominator remains 25.
-
Mixed Number: Therefore, 157/25 as a mixed number is 6 7/25.
Conclusion
Converting an improper fraction like 22/15 to a mixed number (1 7/15) is a straightforward process involving division and understanding the relationship between the numerator, denominator, and remainder. Mastering this skill is essential for various mathematical applications and problem-solving scenarios in everyday life. Remember to always check for simplification opportunities to express your answer in its most efficient form. By understanding the underlying concepts and avoiding common mistakes, you can confidently work with improper fractions and mixed numbers in any context.
Latest Posts
Latest Posts
-
10 Ounces Is Equal To How Many Cups
Apr 22, 2025
-
How Many Feet Is 33 In
Apr 22, 2025
-
How Many Inches Are In 2 80 Ft
Apr 22, 2025
-
32 To The Power Of 2
Apr 22, 2025
-
Find The Inverse Of The Function Y 2x2 4
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 22 15 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.