24 Has How Many 3/4 In It
Kalali
Jul 26, 2025 · 5 min read
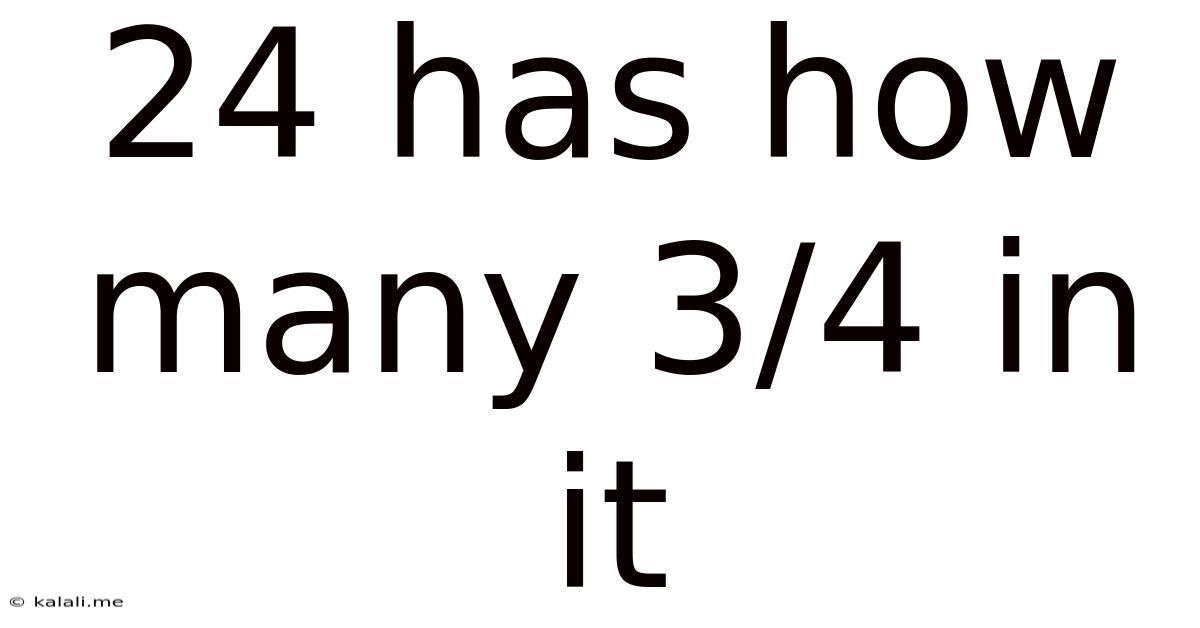
Table of Contents
24 Has How Many 3/4s in It? A Deep Dive into Fractions and Division
This seemingly simple question, "24 has how many 3/4s in it?", opens the door to a fascinating exploration of fractions, division, and the fundamental principles of mathematics. While the answer might seem readily apparent to some, understanding the underlying processes is crucial for mastering more complex mathematical concepts. This article will not only provide the answer but also delve into the methodology, offering a comprehensive guide suitable for both beginners and those looking to refresh their understanding of fractional division.
Meta Description: Discover how many 3/4s are in 24 through a step-by-step explanation. This article explores the concept of dividing whole numbers by fractions, offering a clear understanding of the process and its applications in mathematics. Learn to solve similar problems with confidence.
Understanding the Problem: Fractions and Division
At its core, the question asks us to perform division: We're dividing the whole number 24 by the fraction 3/4. This is a common problem in everyday life, from cooking and construction to finance and data analysis. Understanding how to handle such calculations is essential for navigating numerous real-world scenarios.
Before we proceed, let's refresh our understanding of key concepts:
- Numerator: The top number in a fraction (e.g., 3 in 3/4). It represents the number of parts we have.
- Denominator: The bottom number in a fraction (e.g., 4 in 3/4). It represents the total number of equal parts the whole is divided into.
- Reciprocal: The reciprocal of a fraction is obtained by switching the numerator and the denominator. For example, the reciprocal of 3/4 is 4/3.
Method 1: Converting the Fraction to a Decimal
One approach to solving this problem involves converting the fraction 3/4 into its decimal equivalent. This often simplifies the division process, especially for those more comfortable working with decimals.
-
Convert the fraction to a decimal: To convert 3/4 to a decimal, divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Divide the whole number by the decimal: Now, divide 24 by the decimal equivalent of 3/4: 24 ÷ 0.75 = 32
Therefore, there are 32 instances of 3/4 in 24.
Method 2: Using the Reciprocal and Multiplication
A more mathematically elegant and fundamental approach involves using the reciprocal of the fraction. This method avoids decimal conversions and strengthens your understanding of fraction manipulation.
The core principle here is that dividing by a fraction is equivalent to multiplying by its reciprocal. So, dividing 24 by 3/4 is the same as multiplying 24 by 4/3.
-
Find the reciprocal: The reciprocal of 3/4 is 4/3.
-
Multiply: Multiply 24 by the reciprocal: 24 × (4/3) = (24 × 4) / 3 = 96 / 3
-
Simplify: Simplify the resulting fraction by dividing the numerator (96) by the denominator (3): 96 ÷ 3 = 32
Again, we arrive at the answer: there are 32 instances of 3/4 in 24.
Method 3: Visual Representation
While the previous methods are precise and efficient, visualizing the problem can be particularly helpful for beginners. Imagine a pie chart or a bar graph divided into sections.
-
Visualize the whole: Represent 24 as a whole unit.
-
Represent the fraction: Imagine dividing this whole unit into sections of 3/4.
-
Count the sections: Count how many 3/4 sections fit within the whole unit representing 24. This visual approach reinforces the concept and helps in understanding the underlying principle. You'll find that you can fit 32 sections of 3/4 into the whole of 24.
Extending the Concept: Solving Similar Problems
The methods described above can be applied to solve a wide range of similar problems involving fractional division. Let's consider some examples:
-
How many 2/5 are in 10? Using the reciprocal method: 10 × (5/2) = 25. There are 25 instances of 2/5 in 10.
-
How many 1/3 are in 6? Using the reciprocal method: 6 × (3/1) = 18. There are 18 instances of 1/3 in 6.
-
How many 5/8 are in 20? Using the reciprocal method: 20 × (8/5) = 32. There are 32 instances of 5/8 in 20.
These examples demonstrate the versatility and power of understanding fractional division.
Practical Applications of Fractional Division
The ability to confidently divide whole numbers by fractions is not merely an academic exercise; it has significant practical implications across various fields:
-
Cooking: Scaling recipes up or down requires accurate fractional division. If a recipe calls for 3/4 cup of flour and you want to double it, you'll need to calculate 2 × (3/4).
-
Construction: Measuring and cutting materials accurately often involves working with fractions. If a project requires pieces of wood that are 3/4 of a foot long, and you have a 24-foot board, you'll need to know how many pieces you can cut.
-
Finance: Calculating portions of investments, interest rates, and other financial aspects regularly involves fractional division.
-
Data Analysis: Working with datasets and calculating percentages or proportions frequently requires dividing whole numbers by fractions.
Conclusion: Mastering Fractions for Real-World Success
Understanding how to solve problems like "24 has how many 3/4s in it?" is crucial for anyone seeking mathematical fluency. While the answer – 32 – is straightforward, the journey of understanding the underlying principles of fractional division equips you with a powerful tool applicable to countless real-world situations. By mastering these techniques, you'll not only be able to solve similar problems with confidence but also develop a deeper appreciation for the elegance and practicality of mathematics. Remember to practice regularly to solidify your understanding and build your problem-solving skills. The more you engage with these concepts, the more intuitive and effortless they will become. From cooking to construction, finance to data analysis, the ability to confidently handle fractions empowers you to navigate the complexities of the world around you.
Latest Posts
Latest Posts
-
How Long Does Chicken Broth Last Unopened
Jul 26, 2025
-
How Many Sq In A Box Of Siding
Jul 26, 2025
-
What Is A Half Of One Third
Jul 26, 2025
-
How Many Months Have 5 Weeks In Them
Jul 26, 2025
-
How Long Does It Take To Get Your License Mailed
Jul 26, 2025
Related Post
Thank you for visiting our website which covers about 24 Has How Many 3/4 In It . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.