24 Is What Percent Of 40
Kalali
Apr 13, 2025 · 5 min read
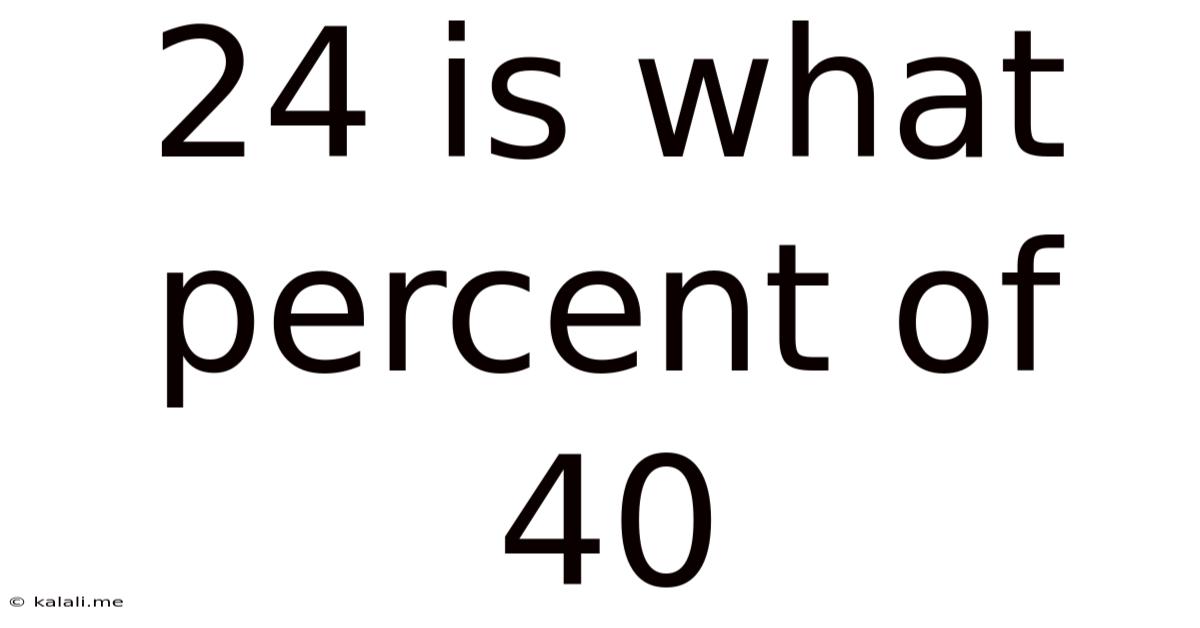
Table of Contents
24 is What Percent of 40? A Comprehensive Guide to Percentage Calculations
This article delves deep into the seemingly simple question: "24 is what percent of 40?" While the answer might seem readily apparent, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting and shopping to complex financial analysis and scientific research. This guide will not only provide the solution but also equip you with the knowledge to tackle similar percentage problems confidently and efficiently. We'll explore different methods of calculation, discuss common pitfalls, and offer practical examples to solidify your understanding.
Meta Description: Learn how to calculate percentages effectively! This comprehensive guide explains how to determine what percent 24 is of 40, covering various methods, common mistakes, and real-world applications. Master percentage calculations today!
Understanding Percentages: The Basics
Before diving into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Understanding this fundamental concept is key to solving any percentage problem. We use percentages to represent proportions, comparing parts to wholes. This makes them invaluable in expressing various data points and trends in clear, concise ways.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percent 24 is of 40 is using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 24 (the number we're considering as a portion of the whole)
- Whole: 40 (the total number)
Let's plug the values into the formula:
(24 / 40) x 100% = 60%
Therefore, 24 is 60% of 40.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
24/40 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
40x = 2400
Now, divide both sides by 40:
x = 2400 / 40 = 60
Therefore, x = 60%, confirming our previous result. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%.
First, express the fraction as a decimal:
24 / 40 = 0.6
Then, multiply the decimal by 100% to obtain the percentage:
0.6 x 100% = 60%
This approach highlights the connection between decimals and percentages, reinforcing the understanding that a percentage is essentially a decimal expressed as a number out of 100. This method is particularly useful when working with calculators or spreadsheets.
Real-World Applications: Why Percentage Calculations Matter
Understanding percentage calculations isn't just an academic exercise; it's a crucial life skill with numerous real-world applications:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is essential for making informed financial decisions, from managing personal finances to analyzing investment portfolios.
-
Shopping: Discounts are often expressed as percentages. Calculating the actual price after a discount requires understanding percentage reductions. For example, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
-
Science and Statistics: Percentages are frequently used to represent data in scientific studies and statistical analysis. They allow for easy comparison of proportions across different groups or samples.
-
Everyday Life: Percentage calculations are frequently used in everyday tasks, such as calculating tips in restaurants, determining the percentage of completion of a project, or understanding survey results.
Common Mistakes to Avoid
While percentage calculations may seem simple, several common mistakes can lead to inaccurate results:
-
Incorrect Order of Operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
-
Misunderstanding the "Part" and "Whole": Clearly identify the part and the whole before applying the formula. Confusing these two values leads to incorrect results.
-
Incorrect Decimal Placement: When converting decimals to percentages, ensure you multiply by 100%. A misplaced decimal point can significantly affect the final answer.
-
Rounding Errors: Be mindful of rounding errors when working with decimals. Avoid premature rounding to maintain accuracy throughout the calculation.
Advanced Percentage Problems: Building on the Fundamentals
Once you've mastered the basics, you can tackle more complex percentage problems. These often involve multiple steps or require solving for an unknown variable. For example:
-
Finding the Whole: If you know that 30% of a number is 60, you can set up an equation to find the whole number. (0.30 * x = 60). Solving for x gives you the whole number.
-
Finding the Percentage Increase or Decrease: Calculating percentage changes involves comparing two values and expressing the difference as a percentage of the original value.
-
Compound Interest Calculations: Compound interest involves calculating interest on both the principal amount and accumulated interest.
Conclusion: Mastering Percentage Calculations for Success
Understanding percentage calculations is a fundamental skill applicable across various fields. This article provided a comprehensive guide to calculating percentages, covering different methods, common mistakes, and real-world applications. By mastering these techniques, you’ll be well-equipped to confidently handle percentage problems and make informed decisions in various aspects of life. Remember, practice is key! The more you practice, the more comfortable and proficient you'll become with percentage calculations. Start by tackling simple problems, gradually progressing to more complex ones. With consistent effort, you'll become adept at this essential mathematical skill. So, next time you encounter a percentage problem, remember the principles outlined in this guide, and you'll be ready to solve it with confidence and accuracy.
Latest Posts
Latest Posts
-
What Is 20 Off Of 150
Apr 14, 2025
-
How Many Hours Is 440 Minutes
Apr 14, 2025
-
235 Divided By 32 With Remainder
Apr 14, 2025
-
10 Liters Equals How Many Gallons
Apr 14, 2025
-
How Many Lines Of Symmetry Does A Rhombus Has
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about 24 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.