24 Is What Percent Of 60
Kalali
Mar 28, 2025 · 4 min read
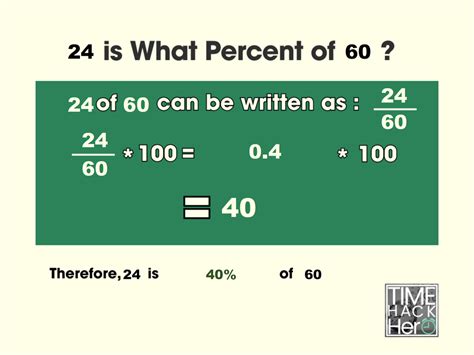
Table of Contents
24 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into the question, "24 is what percent of 60?", providing not only the answer but also a deep dive into the underlying concepts and methods for solving similar percentage problems. We'll explore multiple approaches, ensuring you can confidently tackle any percentage calculation you encounter.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for mastering percentage calculations.
Method 1: Using the Formula
The most common method for calculating percentages involves a simple formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 24
- Whole: 60
Substituting these values into the formula:
(24 / 60) * 100% = 40%
Therefore, 24 is 40% of 60.
Method 2: Proportion Method
This method uses proportions to solve the problem. We set up a proportion where one ratio represents the known values (24/60) and the other represents the unknown percentage (x/100).
24/60 = x/100
To solve for x, we cross-multiply:
24 * 100 = 60 * x
2400 = 60x
x = 2400 / 60
x = 40
Therefore, x = 40%.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, express the problem as a fraction: 24/60
Next, simplify the fraction: 24/60 = 2/5
Now, convert the fraction to a decimal by dividing the numerator by the denominator: 2 ÷ 5 = 0.4
Finally, multiply the decimal by 100% to express it as a percentage: 0.4 * 100% = 40%
Therefore, 24 is 40% of 60.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
1. Financial Calculations:
- Discounts: Calculating the price after a discount is applied. For example, a 20% discount on a $100 item means a savings of $20 (20% of $100).
- Taxes: Determining the amount of tax payable on a purchase. A 6% sales tax on a $50 item means a tax of $3 (6% of $50).
- Interest Rates: Calculating the interest earned on savings accounts or the interest paid on loans.
- Investment Returns: Determining the percentage return on investments.
2. Data Analysis and Statistics:
- Data Representation: Percentages are frequently used to represent data in charts, graphs, and tables, making it easier to understand and compare different sets of information.
- Statistical Analysis: Calculating percentages is essential in many statistical analyses, such as calculating proportions and percentages in surveys and polls.
3. Everyday Life:
- Tip Calculations: Determining the appropriate tip amount in a restaurant.
- Recipe Adjustments: Scaling up or down recipes based on the number of servings.
- Grading Systems: Understanding your performance in school based on percentage grades.
Practice Problems:
To solidify your understanding of percentage calculations, try solving these problems:
- What percentage of 80 is 20?
- 15 is what percent of 75?
- What is 30% of 150?
- If a shirt costs $40 and is discounted by 15%, what is the final price?
- A student scored 45 out of 60 marks on a test. What is their percentage score?
Solutions:
- 25%
- 20%
- 45
- $34
- 75%
Advanced Percentage Concepts:
While the basic percentage calculations are straightforward, several advanced concepts build upon this foundation:
- Percentage Change: Calculating the percentage increase or decrease between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%.
- Compound Interest: Calculating interest earned on both the principal and accumulated interest. This is a more complex calculation involving exponential growth.
- Percentage Points: This represents the absolute difference between two percentages, not the relative difference. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
Conclusion:
Understanding how to calculate percentages is a valuable skill applicable across many fields. By mastering the basic formula and different methods, you can confidently tackle various percentage problems and apply this knowledge to numerous real-world scenarios. Remember to practice regularly to reinforce your understanding and improve your calculation speed and accuracy. With consistent practice, you'll be a percentage pro in no time! This comprehensive guide provides a strong foundation for tackling more complex percentage-related problems and further expands your quantitative reasoning skills. Continue exploring different applications and problem types to build a complete understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Is 160 Degrees Fahrenheit In Celsius
Mar 31, 2025
-
26 7 As A Mixed Number
Mar 31, 2025
-
What Is 56 C In Fahrenheit
Mar 31, 2025
-
How Many Ounces Are In 8 Lb
Mar 31, 2025
-
Which Group Has The Highest Electronegativity
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 24 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
