25 6 As A Mixed Number
Kalali
May 09, 2025 · 2 min read
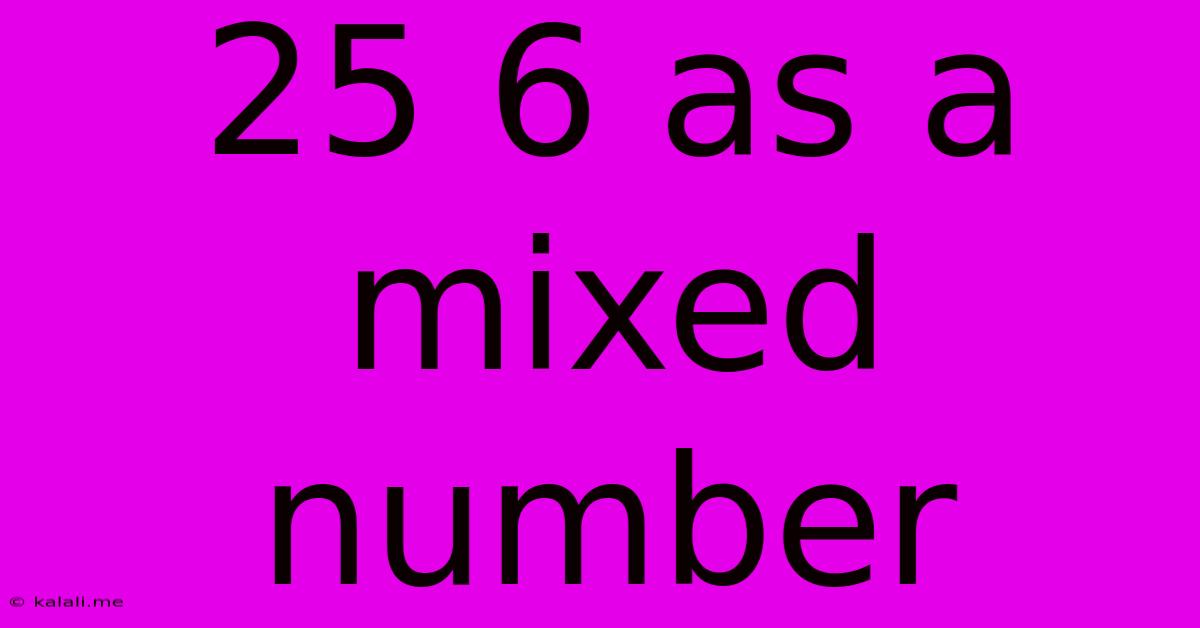
Table of Contents
Converting 25/6 to a Mixed Number: A Step-by-Step Guide
Understanding how to convert improper fractions, like 25/6, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will walk you through the process, explaining the concepts and providing a practical example. We'll also explore the importance of understanding this conversion in various mathematical contexts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (top number) smaller than its denominator (bottom number). For example, 2 ½ is a mixed number, representing two whole units and one-half of another unit.
Converting an Improper Fraction to a Mixed Number
An improper fraction is a fraction where the numerator is larger than or equal to the denominator. 25/6 is an improper fraction because 25 (numerator) is greater than 6 (denominator). To convert it to a mixed number, we need to determine how many times the denominator (6) goes into the numerator (25) and what the remainder is.
Here's the step-by-step process:
- Divide the numerator by the denominator: Divide 25 by 6.
- Find the whole number: The result of the division is 4 with a remainder. The whole number part of your mixed number is 4.
- Determine the new numerator (remainder): The remainder from the division is 1. This becomes the numerator of your fraction.
- Keep the original denominator: The denominator remains the same, which is 6.
- Combine the whole number and the fraction: The final mixed number is 4 1/6.
Therefore, 25/6 as a mixed number is 4 1/6.
Why is this Conversion Important?
Converting improper fractions to mixed numbers is crucial for several reasons:
- Better Understanding: Mixed numbers offer a more intuitive representation of quantities, making them easier to visualize and understand. It's simpler to grasp the concept of "four and one-sixth" than "twenty-five sixths".
- Problem Solving: Many mathematical problems, particularly those involving measurements or real-world applications, require mixed numbers for clear and concise representation.
- Simplification: Mixed numbers can simplify calculations, particularly when dealing with addition and subtraction of fractions.
Practical Applications
Imagine you have 25 slices of pizza and want to divide them equally among 6 people. Using the improper fraction 25/6 doesn't directly tell you how many slices each person gets. However, converting it to the mixed number 4 1/6 clarifies that each person receives 4 whole slices, with 1 slice remaining to be divided further.
Conclusion
Converting improper fractions like 25/6 to mixed numbers is a fundamental mathematical skill with wide-ranging applications. By understanding the process and its importance, you enhance your ability to solve problems and represent quantities in a clearer, more meaningful way. Mastering this conversion is a stepping stone to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Can Anxiety Cause High Red Blood Cell Count
May 09, 2025
-
Cuantos Son 48 Grados Fahrenheit En Centigrados
May 09, 2025
-
3 Inches Equals How Many Centimeters
May 09, 2025
-
32 Is What Percent Of 24
May 09, 2025
-
How Many Kg In 500 Grams
May 09, 2025
Related Post
Thank you for visiting our website which covers about 25 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.