25 Is What Percent Of 100
Kalali
Apr 27, 2025 · 5 min read
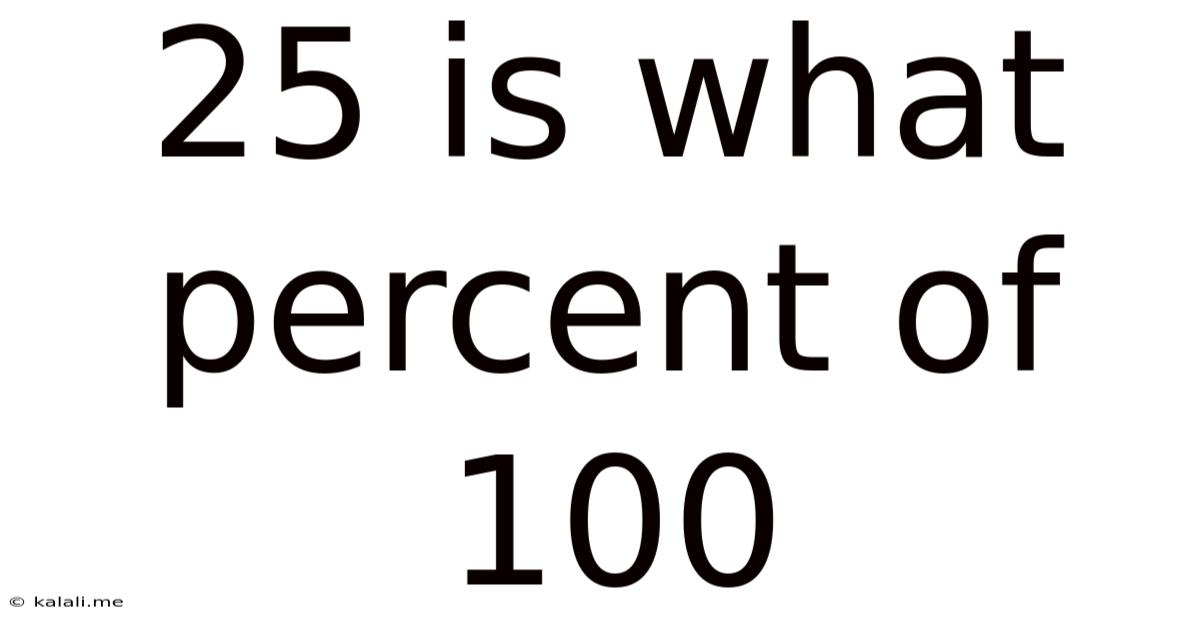
Table of Contents
25 is What Percent of 100? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "25 is what percent of 100?", opens the door to a vast world of mathematical concepts and practical applications. Understanding percentages is fundamental to numerous areas, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only answer the initial question but also delve into the underlying principles of percentages, explore various methods for calculating them, and highlight their real-world significance.
Meta Description: Discover how to calculate percentages, understand the relationship between 25 and 100, and explore the wide-ranging applications of percentage calculations in everyday life and various fields. Learn different methods and practical examples.
Understanding the Concept of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100. This fractional representation is key to understanding percentage calculations. Understanding this foundational concept is crucial before we tackle more complex percentage problems. We can express percentages as decimals, fractions, and ratios – all interchangeable forms representing the same proportional value.
Calculating "25 is What Percent of 100?"
The most straightforward method involves setting up a simple equation:
- Part / Whole = Percentage / 100
In our case:
- 25 / 100 = x / 100
Solving for 'x' (the percentage):
- x = (25 / 100) * 100
- x = 25%
Therefore, 25 is 25% of 100. This might seem self-evident given the definition of percentage, but it's crucial to establish this fundamental calculation before moving on to more complex scenarios. This basic approach forms the foundation for solving all percentage problems.
Alternative Methods for Calculating Percentages
While the equation method is the most common, alternative approaches can be equally effective, especially with mental calculations or when dealing with different percentage problems.
-
Using Decimals: We can convert percentages directly into decimals by dividing by 100. 25% becomes 0.25. Multiplying the decimal by the whole number (100) gives us the part (25). This method is particularly useful when working with calculators or spreadsheets.
-
Using Proportions: The proportion method directly relates the part to the whole. We set up a ratio: 25/100 = x/100. This visually represents the relationship and makes solving for 'x' intuitive. This approach is helpful in understanding the relative sizes and proportions involved.
-
Using Mental Math: For simple percentages like 25% of 100, mental math can be surprisingly efficient. Recognizing that 25% is one-quarter (1/4) of 100 simplifies the calculation immediately. This method enhances calculation speed and number sense.
Real-World Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple mathematical exercises. It’s an essential skill applicable across various aspects of life:
-
Financial Literacy: Understanding percentages is fundamental to managing personal finances. Calculating interest rates on loans, savings accounts, and credit cards relies heavily on percentage calculations. Analyzing investment returns, understanding tax rates, and budgeting effectively all involve working with percentages. Understanding discounts, sales tax, and tips at restaurants requires quick percentage calculations.
-
Business and Economics: In business, percentages are ubiquitous. Profit margins, market share analysis, growth rates, and sales figures are all expressed as percentages. Businesses use percentages to track performance, make strategic decisions, and compare their progress against competitors. Economic indicators like inflation, unemployment, and GDP growth are typically expressed as percentages.
-
Science and Statistics: Scientists and statisticians use percentages extensively to represent data and analyze results. Presenting experimental results, analyzing survey data, and calculating probabilities all involve percentage calculations. Understanding statistical significance and error margins often requires manipulating percentages. Percentage changes in scientific measurements and experimental results are crucial for analysis and interpretation.
-
Everyday Life: Beyond formal contexts, we encounter percentages daily. Reading nutrition labels on food products, understanding discounts at stores, calculating tips in restaurants, and interpreting weather forecasts (e.g., chance of rain) all involve percentages.
Advanced Percentage Calculations
While the "25 is what percent of 100" question provides a basic understanding, more advanced calculations require additional steps:
-
Finding the Percentage Increase or Decrease: This involves calculating the change in value relative to the original value. For example, if a price increases from $100 to $125, the percentage increase is calculated as [(125-100)/100] * 100% = 25%.
-
Calculating Percentage Change Over Time: This requires understanding the initial and final values over a specific period. Tracking stock prices, population growth, or economic indicators often involves calculating percentage changes over time.
-
Working with Compound Percentages: This involves applying a percentage to a value, then applying the percentage again to the new, increased value. Compound interest, for instance, uses this method.
-
Solving for the Whole or the Part: Problems might ask for the whole amount given a percentage and a part, or vice versa. This requires rearranging the basic percentage equation.
Practical Examples of Percentage Calculations
Let's explore some more complex scenarios to solidify our understanding:
Example 1: A shirt is discounted by 30% from its original price of $50. What is the sale price?
- First, calculate the discount amount: 30% of $50 = (30/100) * $50 = $15
- Then, subtract the discount from the original price: $50 - $15 = $35
- The sale price is $35.
Example 2: A student scored 80 out of 100 on a test. What is their percentage score?
- Use the equation: Part / Whole = Percentage / 100
- 80 / 100 = x / 100
- x = 80%
- The student scored 80%.
Example 3: A town's population increased by 15% to 2300 people. What was the original population?
- Let 'x' be the original population.
- x + 0.15x = 2300
- 1.15x = 2300
- x = 2300 / 1.15
- x ≈ 2000
- The original population was approximately 2000.
These examples showcase the versatility and practical applications of percentage calculations in various real-world situations.
Conclusion
The seemingly simple question, "25 is what percent of 100?", serves as a springboard to understanding the broader significance of percentage calculations. From managing personal finances and analyzing business data to comprehending scientific results and navigating everyday life, mastering percentages is an indispensable skill. This article provides a comprehensive overview of percentage calculations, including various methods, practical examples, and advanced applications, equipping readers with the knowledge to confidently tackle a wide range of percentage-related problems. Remember that practice is key; the more you work with percentages, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
X 2 X 2 3x 1
Apr 28, 2025
-
How Much Is 75ml In Oz
Apr 28, 2025
-
120 Centimeters Equals How Many Inches
Apr 28, 2025
-
Write The Chemical Equation For Cellular Respiration
Apr 28, 2025
-
What Is 40 Degrees C In F
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.