25 Is What Percent Of 20
Kalali
Apr 22, 2025 · 5 min read
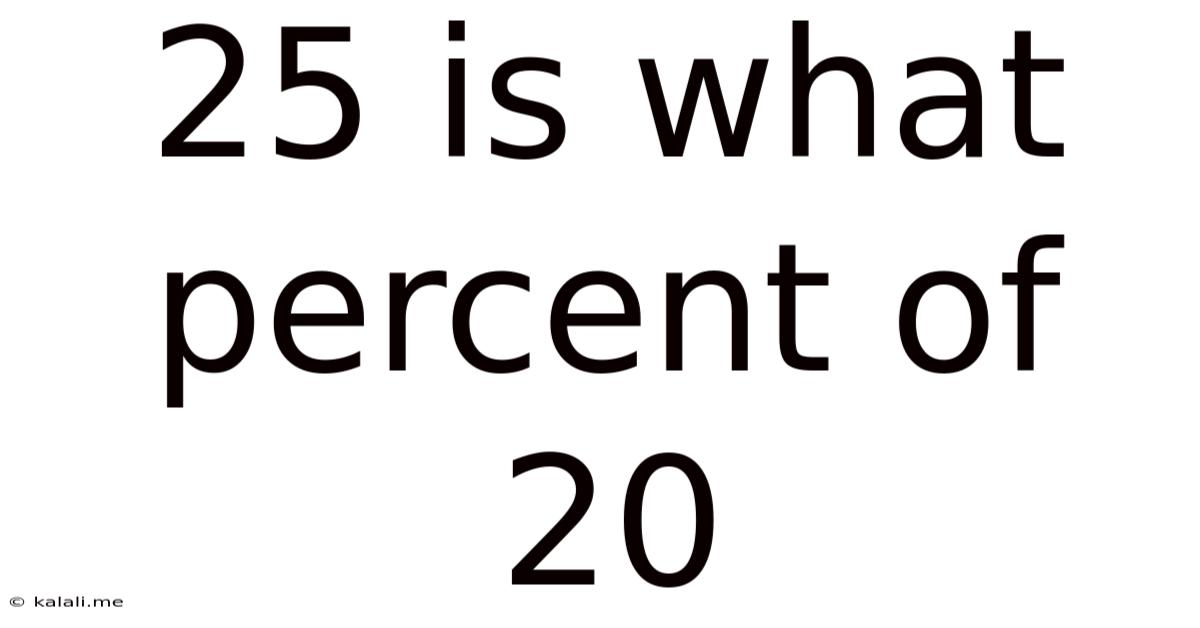
Table of Contents
25 is What Percent of 20? Unpacking Percentages and Their Applications
This seemingly simple question, "25 is what percent of 20?", opens the door to a broader understanding of percentages, their calculations, and their widespread applications in various fields. While the direct answer might seem straightforward, exploring the underlying concepts provides a much richer understanding and equips you with the tools to tackle more complex percentage problems. This article will not only solve the problem but also delve into the methods, practical examples, and the broader implications of percentage calculations.
Meta Description: Learn how to calculate percentages and understand the concept of "25 is what percent of 20?". This article provides a comprehensive guide with examples, real-world applications, and advanced techniques.
Understanding Percentages:
Percentages are a fundamental concept in mathematics and are used extensively in everyday life. A percentage represents a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5 as a decimal. Understanding this basic definition is crucial for solving percentage problems.
Methods for Calculating Percentages:
There are several ways to calculate percentages, each with its advantages depending on the context and the complexity of the problem. Let's explore the most common methods:
1. The Formulaic Approach:
The most direct method involves using the percentage formula:
(Part / Whole) * 100 = Percentage
In our specific problem, "25 is what percent of 20?", we identify:
- Part: 25
- Whole: 20
Substituting these values into the formula:
(25 / 20) * 100 = 125%
Therefore, 25 is 125% of 20. This result might seem counterintuitive at first, as the part (25) is larger than the whole (20). However, this simply indicates that 25 represents more than the entirety of 20 – it's 125% of it.
2. Using Proportions:
Proportions offer another effective way to solve percentage problems. A proportion sets up an equivalence between two ratios. We can represent our problem as:
25 / 20 = x / 100
where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
20x = 2500
x = 2500 / 20
x = 125
Therefore, x = 125%, confirming the result from the formulaic approach.
3. Decimal Conversion:
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
25 / 20 = 1.25
1.25 * 100 = 125%
This method is particularly useful when dealing with decimals or fractions in the initial problem statement.
Interpreting the Result: 125%
The answer, 125%, indicates that 25 exceeds 20 by 25%. It's 125% of the original value (20). This concept is crucial in understanding percentage increases, which we'll explore further.
Real-World Applications of Percentage Calculations:
Percentage calculations are ubiquitous in various aspects of life:
1. Finance and Business:
- Profit margins: Businesses use percentages to calculate profit margins, comparing profit to revenue.
- Interest rates: Banks and financial institutions use percentages to express interest rates on loans and savings accounts.
- Discounts and Sales: Retailers use percentages to advertise discounts and sales on products.
- Investment returns: Investors use percentages to track the return on investment (ROI) of their portfolios. A 10% ROI means the investment grew by 10%.
- Tax calculations: Tax rates are expressed as percentages of income or the value of goods and services.
2. Science and Statistics:
- Data analysis: Percentages are frequently used to represent proportions and distributions in data analysis. For example, expressing the percentage of survey respondents who prefer a particular product.
- Scientific experiments: Results from experiments are often presented as percentages to represent the rate of success or failure.
- Probability: Percentages are used to express probabilities, indicating the likelihood of an event occurring.
3. Everyday Life:
- Tip calculations: People use percentages to calculate tips in restaurants. A 15% tip on a $50 meal is $7.50.
- Recipe adjustments: When cooking, percentages can help in adjusting recipe quantities for different numbers of servings.
- Grading systems: Many educational systems use percentages to represent grades and scores on assessments.
- Sales tax: Sales tax is expressed as a percentage of the purchase price.
Advanced Percentage Calculations:
While our initial problem was relatively straightforward, percentage calculations can become more complex. Let's explore some scenarios:
1. Percentage Increase and Decrease:
Calculating percentage increases and decreases requires an understanding of the initial value and the change. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100
Similarly, the formula for percentage decrease is:
[(Old Value - New Value) / Old Value] * 100
For instance, if a price increases from $20 to $25, the percentage increase is:
[(25 - 20) / 20] * 100 = 25%
2. Compounding Percentages:
Compounding involves applying a percentage change to a value repeatedly over time. This is common in finance, where interest is often compounded annually or more frequently.
3. Percentage Points vs. Percentage Change:
It's essential to distinguish between percentage points and percentage change. A percentage point refers to the arithmetic difference between two percentages. For example, if the interest rate increases from 5% to 10%, it's a 5 percentage point increase, not a 100% increase.
Conclusion:
The question, "25 is what percent of 20?", while seemingly simple, unveils a deeper understanding of percentage calculations and their applications. Mastering percentage calculations is vital for navigating various aspects of life, from personal finance to scientific analyses. By utilizing the formulas, proportions, and decimal conversion methods, we can effectively solve a wide array of percentage problems and gain valuable insights into the data at hand. Remember to consider the context, interpret results carefully, and differentiate between percentage change and percentage points for a comprehensive understanding. The ability to calculate and interpret percentages is a fundamental skill with far-reaching implications in a data-driven world.
Latest Posts
Latest Posts
-
32 Cm Equals How Many Inches
Apr 22, 2025
-
How Many Hours Is 375 Minutes
Apr 22, 2025
-
Least Common Multiple 4 And 8
Apr 22, 2025
-
How Many Hours Is 205 Minutes
Apr 22, 2025
-
What Is 85 Degrees In Celsius
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.