25 Is What Percent Of 500
Kalali
Apr 14, 2025 · 5 min read
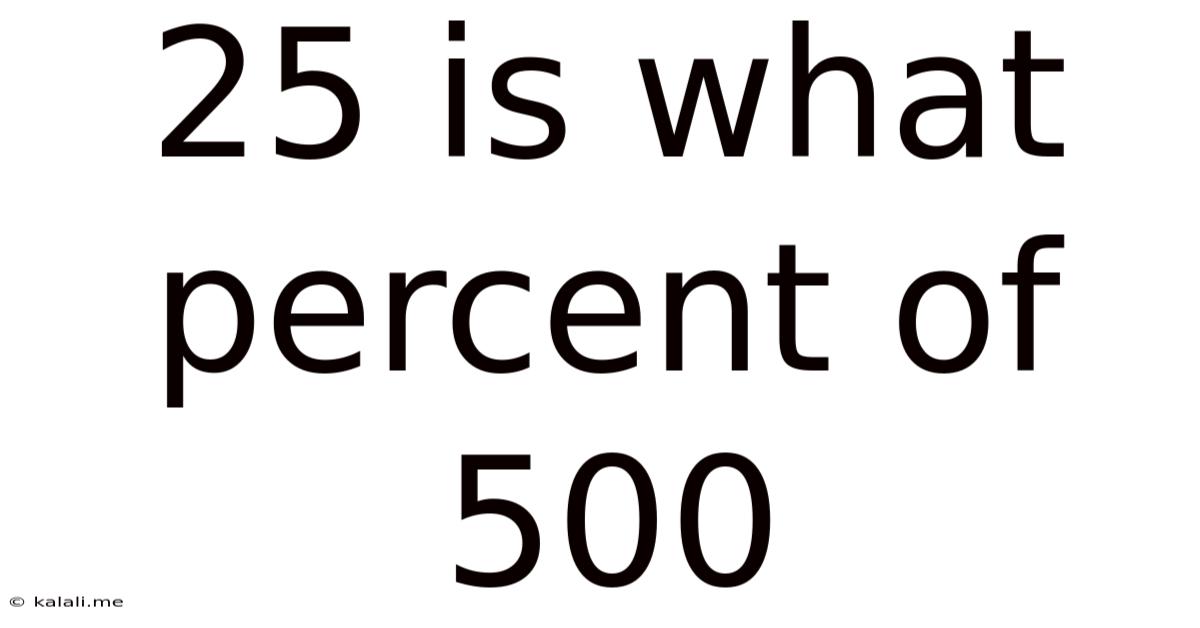
Table of Contents
25 is What Percent of 500? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to solve percentage problems efficiently is crucial for both personal and professional success. This article delves deep into the question, "25 is what percent of 500?", providing not only the answer but also a comprehensive explanation of the underlying principles and various methods for solving percentage problems. We'll explore different approaches, including using formulas, proportions, and even mental math techniques. By the end, you'll be confident in tackling any percentage calculation you encounter.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "25 is what percent of 500?". This guide covers multiple methods, including formulas, proportions, and mental math tricks, equipping you with the skills to tackle various percentage problems.
Understanding Percentages: The Basics
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The term "percent" itself originates from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This foundational understanding is crucial for all percentage calculations.
Understanding the relationship between fractions, decimals, and percentages is vital. They are all different ways of expressing the same value. For instance:
- Fraction: 1/4
- Decimal: 0.25
- Percentage: 25%
These representations are interchangeable, and converting between them is often a necessary step in solving percentage problems.
Method 1: Using the Percentage Formula
The most common method for calculating percentages involves using a straightforward formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 25
- Whole: 500
Plugging these values into the formula:
(25 / 500) * 100% = 5%
Therefore, 25 is 5% of 500.
Method 2: Setting up a Proportion
Proportions offer another effective way to solve percentage problems. A proportion is a statement that equates two ratios. We can set up a proportion using the following structure:
Part / Whole = Percentage / 100
Again, using our values:
25 / 500 = x / 100
To solve for 'x' (the percentage), we cross-multiply:
25 * 100 = 500 * x
2500 = 500x
x = 2500 / 500
x = 5
Therefore, 25 is 5% of 500. This method demonstrates the relationship between the parts and the whole in a clear and visual way.
Method 3: Using Decimal Equivalents
This method leverages the relationship between percentages and decimals. As mentioned earlier, 25% is equivalent to the decimal 0.25. We can express the problem as follows:
0.25 * 500 = x
Solving for x:
x = 125
This doesn't directly answer the question "25 is what percent of 500?", but it shows that 25% of 500 equals 125. To find the percentage that 25 represents of 500, we need to divide 25 by 500, and then multiply by 100%:
(25/500) * 100% = 5%
Method 4: Mental Math Techniques
For simpler percentage problems, mental math can be surprisingly efficient. Notice that 500 is 20 times 25 (500 / 25 = 20). Since we're looking for the percentage that 25 represents of 500, and 25 goes into 500 twenty times, we can easily deduce that 25 represents 1/20th of 500. To convert this fraction into a percentage, we simply divide 1 by 20 (which equals 0.05) and multiply by 100% to get 5%.
Expanding the Understanding: Variations and Applications
The core principles demonstrated above can be applied to a wide array of percentage problems. Let's explore some variations:
- Finding the Whole: If the problem were "5% of what number is 25?", we would rearrange the formula. We’d solve (25/x) * 100% = 5%, which gives us x=500.
- Finding the Part: A problem like, "What is 5% of 500?" requires a simple calculation: 0.05 * 500 = 25.
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values, dividing by the original value, and multiplying by 100%. For example, if a price increases from $100 to $120, the percentage increase is ((120-100)/100) * 100% = 20%.
- Real-world applications: Percentage calculations are vital in many fields, including finance (interest rates, discounts), statistics (data analysis), science (concentration calculations), and more.
Common Mistakes to Avoid
When working with percentages, several common pitfalls can lead to incorrect results. Here are a few to watch out for:
- Confusing Part and Whole: Ensure you correctly identify the "part" and the "whole" in the problem.
- Incorrect Formula Application: Double-check that you're using the correct formula and plugging in values accurately.
- Calculation Errors: Simple arithmetic mistakes are easily made; use a calculator or verify your calculations when needed.
- Misinterpreting the Question: Carefully read the problem to ensure you understand what is being asked.
Practical Exercises
To solidify your understanding, try these practice problems:
- What percent of 80 is 20?
- 15 is what percent of 75?
- 30% of what number is 60?
- What is 25% of 200?
- A shirt was originally priced at $50 and is now on sale for $40. What is the percentage discount?
By working through these examples, and applying the different methods discussed in this article, you will strengthen your ability to confidently tackle any percentage calculation. Remember that understanding the underlying principles is key to mastering this essential mathematical skill. Whether you're using the formula, proportions, decimals, or even mental math, the ability to calculate percentages is a versatile tool applicable to numerous aspects of life.
Latest Posts
Latest Posts
-
What Is 3 And 1 8 As A Decimal
Apr 15, 2025
-
6 Out Of 10 Percentage Grade
Apr 15, 2025
-
What Is 8 Out Of 9 As A Percentage
Apr 15, 2025
-
A Bunch Of Amino Acids Attached Together Is Called A
Apr 15, 2025
-
Temperature At Which Water Vapor Condenses
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.