25 Is What Percent Of 60
Kalali
Apr 10, 2025 · 5 min read
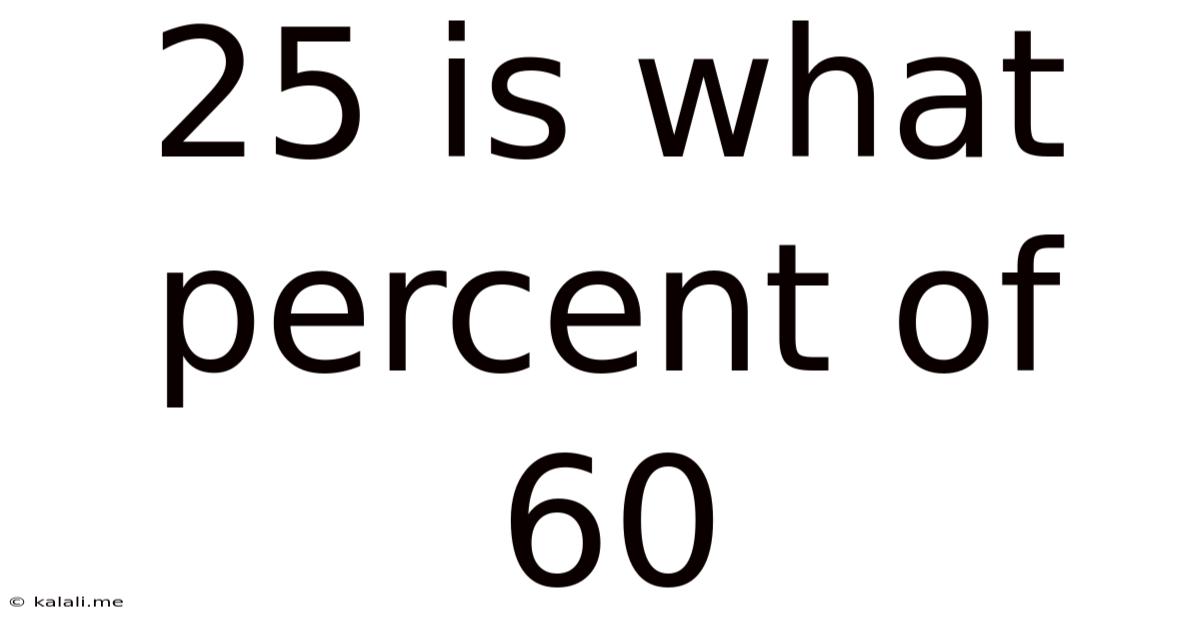
Table of Contents
25 is What Percent of 60? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "25 is what percent of 60?", opens the door to a broader understanding of percentages, their applications, and how to solve them efficiently. This comprehensive guide will not only answer the question but also equip you with the knowledge and skills to tackle similar percentage problems with confidence. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into different methods of solving percentage problems, offering practical examples and explanations along the way.
Understanding Percentages:
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to represent proportions, ratios, and changes in values.
Method 1: Using the Percentage Formula
The most straightforward way to solve "25 is what percent of 60?" is using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 25 (the number we're considering as a part of the whole)
- Whole: 60 (the total amount)
Let's plug the values into the formula:
(25 / 60) x 100% = 41.67%
Therefore, 25 is 41.67% of 60.
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
25 / 60 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
25 * 100 = 60 * x
2500 = 60x
x = 2500 / 60
x ≈ 41.67
Again, we arrive at the answer: 25 is approximately 41.67% of 60.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction: 25/60
Next, divide the numerator (25) by the denominator (60): 25 ÷ 60 ≈ 0.4167
Finally, multiply the decimal by 100%: 0.4167 x 100% = 41.67%
This confirms that 25 is approximately 41.67% of 60.
Practical Applications of Percentage Calculations:
Understanding percentage calculations is essential in numerous real-world situations. Here are some examples:
-
Discounts: A store offers a 20% discount on an item priced at $100. To calculate the discount amount, you'd find 20% of $100: (20/100) x $100 = $20. The discounted price would be $100 - $20 = $80.
-
Taxes: If the sales tax is 8% and you buy an item for $50, the tax amount is (8/100) x $50 = $4. The total cost, including tax, would be $50 + $4 = $54.
-
Tips: Calculating a tip in a restaurant often involves percentages. For instance, a 15% tip on a $75 bill is (15/100) x $75 = $11.25.
-
Financial Analysis: Percentages are frequently used in financial statements to show growth rates, profit margins, and other key metrics. For example, a company's revenue increased by 10% compared to the previous year.
-
Data Analysis: Percentages are used to represent data in charts and graphs, making it easier to visualize and understand trends and patterns. For example, analyzing survey results often involves calculating the percentage of respondents who chose each option.
-
Grade Calculation: In educational settings, percentages are widely used to represent student grades. For example, scoring 80 out of 100 on an exam translates to an 80% grade.
-
Interest Rates: Understanding interest rates involves percentage calculations. For instance, a 5% interest rate on a loan means you pay 5% of the principal amount as interest each year.
Advanced Percentage Problems:
Let's explore some more complex percentage scenarios and how to solve them:
Scenario 1: Finding the Whole when given the Percentage and Part
Problem: 30 is 60% of what number?
Here, we need to rearrange the formula:
(Part / Percentage) x 100 = Whole
(30 / 60) x 100 = 50
Therefore, 30 is 60% of 50.
Scenario 2: Finding the Percentage Increase or Decrease
Problem: A product's price increased from $50 to $60. What is the percentage increase?
- Find the difference: $60 - $50 = $10
- Divide the difference by the original price: $10 / $50 = 0.2
- Multiply by 100% to express as a percentage: 0.2 x 100% = 20%
The price increased by 20%.
Scenario 3: Successive Percentage Changes
Problem: A price is increased by 10% and then decreased by 10%. Is the final price the same as the original price?
No. Successive percentage changes don't cancel out. Let's illustrate with an example:
Original price: $100
10% increase: $100 + ($100 x 0.10) = $110
10% decrease from $110: $110 - ($110 x 0.10) = $99
The final price is $99, not the original $100. This is because the 10% decrease is calculated on the increased price of $110, not the original $100.
Tips for Mastering Percentage Calculations:
-
Practice Regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
-
Understand the Formula: Make sure you thoroughly understand the basic percentage formula and how to rearrange it to solve for different variables.
-
Use Calculators Effectively: While it's important to understand the underlying concepts, using a calculator can help you solve complex problems more quickly and accurately.
-
Check Your Work: Always double-check your calculations to avoid errors.
-
Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps.
Conclusion:
This comprehensive guide has explored various methods for solving percentage problems, demonstrating their wide-ranging applications in everyday life. By mastering these techniques, you can confidently tackle a variety of percentage calculations, enhancing your analytical skills and making informed decisions in various contexts. Remember, consistent practice is key to building proficiency in this crucial mathematical skill. From calculating discounts to analyzing financial data, understanding percentages is a valuable tool that will serve you well in numerous aspects of life. Now, you not only know that 25 is 41.67% of 60, but you also possess the tools to solve a wide range of percentage problems with ease and accuracy.
Latest Posts
Latest Posts
-
How Much Is 39 Degrees Fahrenheit In Celsius
Apr 18, 2025
-
What Does A Open Circle Mean On A Number Line
Apr 18, 2025
-
Simulations Of Compound Events I Ready
Apr 18, 2025
-
How Many Atoms In Face Centered Cubic
Apr 18, 2025
-
6 To The Power Of Twoxtwelve
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.