25 Is What Percent Of 70
Kalali
Apr 11, 2025 · 5 min read
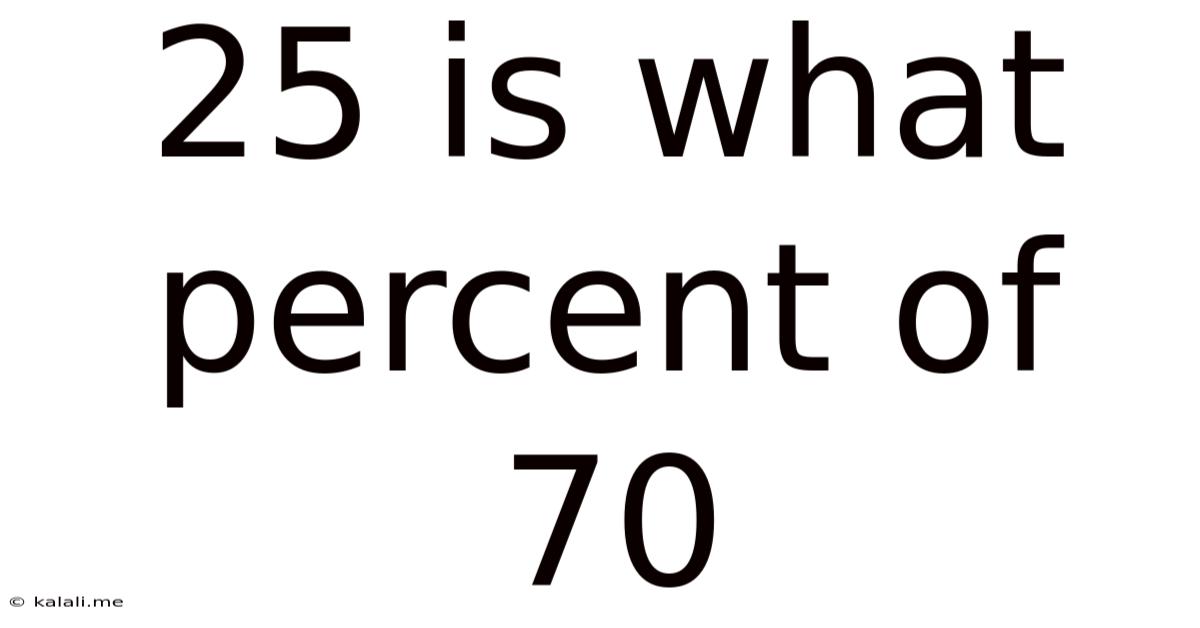
Table of Contents
25 is What Percent of 70? A Deep Dive into Percentage Calculations and Real-World Applications
Meta Description: Learn how to calculate percentages, specifically solving the problem "25 is what percent of 70?". This guide explores the underlying math, provides step-by-step solutions, and shows practical applications of percentage calculations in everyday life and various fields.
This seemingly simple question, "25 is what percent of 70?", opens a door to a fundamental mathematical concept with far-reaching applications. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will not only provide the answer but also delve into the methodology, explore different approaches to solving the problem, and illustrate its relevance in diverse real-world scenarios.
Understanding Percentages: A Foundational Concept
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Percentages are a convenient way to represent proportions and ratios, making comparisons and calculations easier.
Method 1: Using the Percentage Formula
The most straightforward method to solve "25 is what percent of 70?" is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 25 (the number we want to express as a percentage)
- Whole: 70 (the total number)
Let's plug these values into the formula:
(25 / 70) * 100% = ≈ 35.71%
Therefore, 25 is approximately 35.71% of 70.
Method 2: Setting up a Proportion
Another way to solve this problem is by setting up a proportion. A proportion is a statement that two ratios are equal. We can represent the problem as:
25/70 = x/100
where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
25 * 100 = 70 * x
2500 = 70x
x = 2500 / 70
x ≈ 35.71
Again, we find that 25 is approximately 35.71% of 70.
Method 3: Using Decimal Conversion
We can also solve this problem by first converting the fraction 25/70 into a decimal and then multiplying by 100% to express it as a percentage.
25 / 70 ≈ 0.3571
0.3571 * 100% ≈ 35.71%
This method provides the same result: 25 is approximately 35.71% of 70.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world situations. Here are just a few examples:
- Retail and Sales: Calculating discounts, sales tax, profit margins, and markups. For example, a 20% discount on a $100 item would be calculated as (20/100) * $100 = $20.
- Finance: Understanding interest rates, loan repayments, investment returns, and tax deductions. Knowing how to calculate percentage changes in your investment portfolio is critical for financial planning.
- Science and Statistics: Representing data in graphs and charts, calculating statistical measures like percentages, and analyzing experimental results. Percentage changes are used extensively to compare data sets over time.
- Everyday Life: Calculating tips in restaurants, determining the percentage of ingredients in recipes, understanding nutritional information on food labels, and working with ratios and proportions.
- Education: Calculating grades, understanding test scores, and analyzing performance metrics. Percentage scores are a standard way to evaluate student performance.
- Data Analysis: Percentage changes are a useful tool in interpreting data trends and patterns. Whether you're analyzing web traffic, sales figures or social media engagement, understanding percentage increases or decreases helps you to draw insightful conclusions.
- Healthcare: Calculating dosages, analyzing the success rate of treatments, and interpreting diagnostic test results. Many medical calculations and interpretations rely heavily on percentage calculations.
Beyond the Basic Calculation: Exploring Percentage Change and Increase/Decrease
While the question focuses on finding a percentage of a whole, it's also useful to understand how to calculate percentage changes. This is especially relevant when comparing values over time or assessing growth or decline.
Percentage Change Formula:
[(New Value - Old Value) / Old Value] * 100%
For example, if a stock price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100% = 20%
Similarly, if the price decreases from $60 to $50, the percentage decrease is:
[(50 - 60) / 60] * 100% = -16.67%
Understanding these calculations is crucial in many financial and analytical contexts.
Advanced Applications: Compound Interest and Exponential Growth
Percentages are also fundamental to understanding concepts like compound interest, where interest earned is added to the principal amount, leading to exponential growth. This is a key concept in finance and investment, helping to predict future values based on a given interest rate.
The formula for compound interest is:
A = P (1 + r/n)^(nt)
where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Mastering percentage calculations is a cornerstone of financial literacy, allowing for informed decision-making regarding investments, loans, and budgeting.
Conclusion: The Importance of Percentage Understanding
The seemingly simple problem, "25 is what percent of 70?", underscores the importance of a firm grasp of percentage calculations. This fundamental skill has far-reaching implications across numerous fields and everyday life. By mastering the various methods presented in this article, you'll be better equipped to tackle percentage-related challenges, making informed decisions and enhancing your problem-solving abilities. From interpreting financial statements to analyzing data sets, the ability to confidently work with percentages is a valuable asset in both professional and personal contexts. Remember to practice these techniques regularly to build fluency and confidence in your calculations. The more you practice, the more natural and intuitive these calculations will become.
Latest Posts
Latest Posts
-
How Many Inches Is 20 Meters
Apr 18, 2025
-
54 Is What Percent Of 60
Apr 18, 2025
-
What Is A Verbal Expression In Math
Apr 18, 2025
-
Does Liquid Have A Definite Volume
Apr 18, 2025
-
How Many Cups In 64 Ounces Of Water
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percent Of 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.