25 Is What Percentage Of 75
Kalali
Apr 06, 2025 · 5 min read
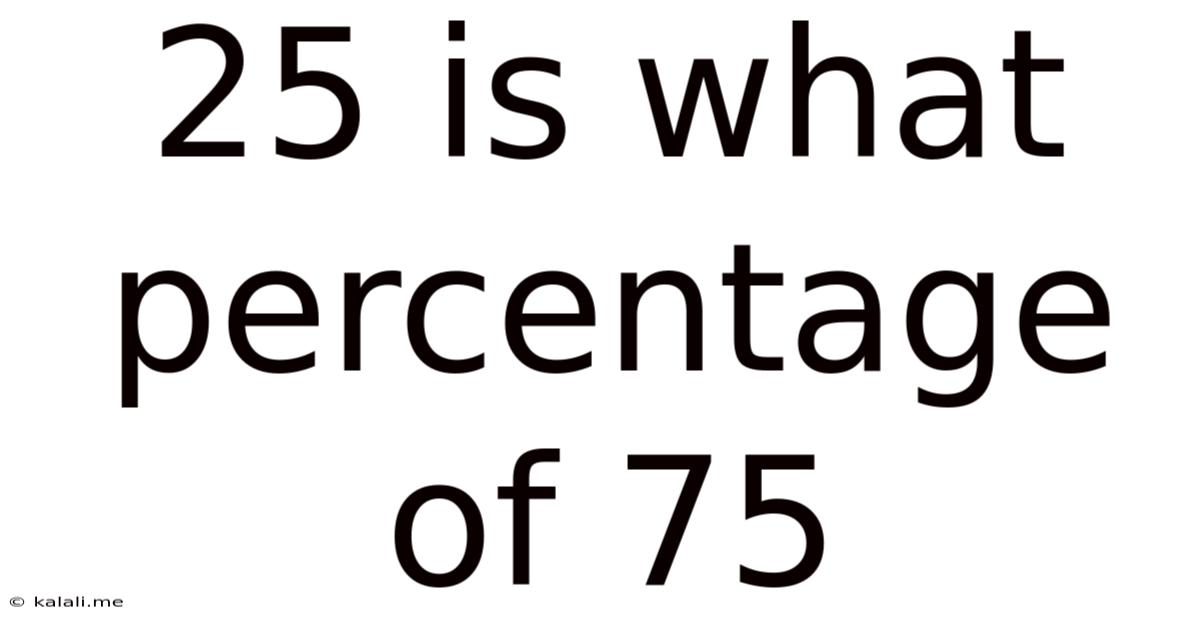
Table of Contents
- 25 Is What Percentage Of 75
- Table of Contents
- 25 is What Percentage of 75? A Comprehensive Guide to Percentage Calculations
- Understanding Percentages: The Fundamentals
- Calculating Percentages: The Three Key Approaches
- Beyond the Basic Calculation: Real-World Applications
- Advanced Percentage Problems: Building on the Fundamentals
- Mastering Percentage Calculations: Tips and Tricks
- Conclusion: Unlocking the Power of Percentages
- Latest Posts
- Latest Posts
- Related Post
25 is What Percentage of 75? A Comprehensive Guide to Percentage Calculations
The question "25 is what percentage of 75?" might seem simple at first glance. However, understanding how to solve this problem unlocks a crucial skill applicable to countless real-world situations, from calculating discounts and taxes to understanding financial reports and analyzing data. This comprehensive guide will not only answer the question directly but also delve into the underlying principles of percentage calculations, providing you with the tools to tackle any similar problem with confidence.
Understanding Percentages: The Fundamentals
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred," indicating how many parts of a whole are being considered. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Percentages are incredibly useful because they provide a standardized way to compare proportions. Whether you're comparing sales figures, student test scores, or the ingredients in a recipe, percentages offer a common denominator for easy understanding and analysis.
Calculating Percentages: The Three Key Approaches
There are three primary methods for calculating percentages:
1. The Formula Method: This is the most direct and commonly used method. The formula is:
(Part / Whole) * 100 = Percentage
In our case, 25 is the "part" and 75 is the "whole." Plugging these values into the formula, we get:
(25 / 75) * 100 = 33.33%
Therefore, 25 is 33.33% of 75.
2. The Proportion Method: This method uses proportions to solve for the unknown percentage. We can set up a proportion as follows:
25/75 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
25 * 100 = 75 * x
2500 = 75x
x = 2500 / 75
x = 33.33%
This method reinforces the concept of ratios and proportions, providing a different perspective on the problem.
3. The Decimal Method: This method involves converting the fraction to a decimal first, then multiplying by 100 to express it as a percentage.
25 / 75 = 0.3333...
0.3333... * 100 = 33.33%
This method highlights the connection between fractions, decimals, and percentages.
Beyond the Basic Calculation: Real-World Applications
The ability to calculate percentages has wide-ranging applications across numerous fields. Here are a few examples:
1. Finance and Budgeting: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions, whether it's managing personal finances or analyzing complex investment portfolios.
2. Sales and Marketing: Tracking sales growth, conversion rates, customer acquisition costs, and return on investment (ROI) all involve percentage calculations. Marketers use percentages to measure campaign effectiveness, analyze customer behavior, and optimize marketing strategies.
3. Data Analysis and Statistics: Percentages are fundamental to statistical analysis. Representing data as percentages helps simplify comparisons and draw meaningful conclusions from complex datasets. This is vital in fields like research, healthcare, and social sciences.
4. Education and Assessments: Grade calculations, test scores, and performance evaluations often use percentages to represent academic progress and achievements. Understanding percentages helps students track their performance and identify areas for improvement.
5. Everyday Life: Calculating tips in restaurants, understanding sale discounts in stores, or determining the percentage of ingredients in a recipe all involve percentage calculations. It's a skill that enhances everyday decision-making.
Advanced Percentage Problems: Building on the Fundamentals
While the problem "25 is what percentage of 75?" is relatively straightforward, understanding the underlying principles allows you to tackle more complex percentage problems. Here are some examples:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example: "30% of what number is 15?" You would use the formula: (Part / Percentage) * 100 = Whole.
-
Finding the Part: If you know the percentage and the whole, you can calculate the part. For example: "What is 20% of 100?" You would use the formula: (Percentage/100) * Whole = Part.
-
Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values and expressing it as a percentage of the original value. For example, if a price increases from $50 to $60, the percentage increase is calculated as: [(New Value - Old Value) / Old Value] * 100.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It requires understanding exponential growth and applying percentage calculations iteratively.
-
Percentage Points vs. Percentage Change: It's important to distinguish between these two concepts. Percentage points represent the arithmetic difference between two percentages, while percentage change represents the relative difference. For example, if a rate increases from 10% to 15%, the increase is 5 percentage points, but the percentage change is 50%.
Mastering Percentage Calculations: Tips and Tricks
To master percentage calculations, consider these helpful tips:
-
Practice Regularly: The more you practice, the more comfortable you'll become with the different methods and their applications.
-
Use a Calculator: While mental calculations can be helpful for simpler problems, a calculator is invaluable for more complex scenarios.
-
Understand the Context: Always consider the context of the problem to ensure you're applying the correct method and interpreting the results correctly.
-
Break Down Complex Problems: Large or complex problems can often be broken down into smaller, manageable steps.
-
Check Your Work: Always double-check your calculations to avoid errors.
Conclusion: Unlocking the Power of Percentages
The simple question, "25 is what percentage of 75?" serves as a gateway to understanding a powerful tool used across various disciplines. By mastering percentage calculations, you equip yourself with a vital skill that enhances your ability to analyze data, make informed decisions, and navigate the complexities of the modern world. From financial planning to data analysis and everyday life, the ability to confidently work with percentages is an invaluable asset. Remember to practice regularly, understand the different methods, and always check your work to ensure accuracy. With consistent practice, you'll become proficient in handling any percentage problem you encounter.
Latest Posts
Latest Posts
-
What Two Characteristics Of Living Things Do Viruses Exhibit
Apr 11, 2025
-
12 Out Of 20 Is What Percent
Apr 11, 2025
-
What Is 44 Inches Tall In Feet
Apr 11, 2025
-
What Is 20 Fahrenheit In Celsius
Apr 11, 2025
-
How Much Is 27 Celsius In Fahrenheit
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about 25 Is What Percentage Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.