25 Of 75 Is What Percent
Kalali
Apr 11, 2025 · 5 min read
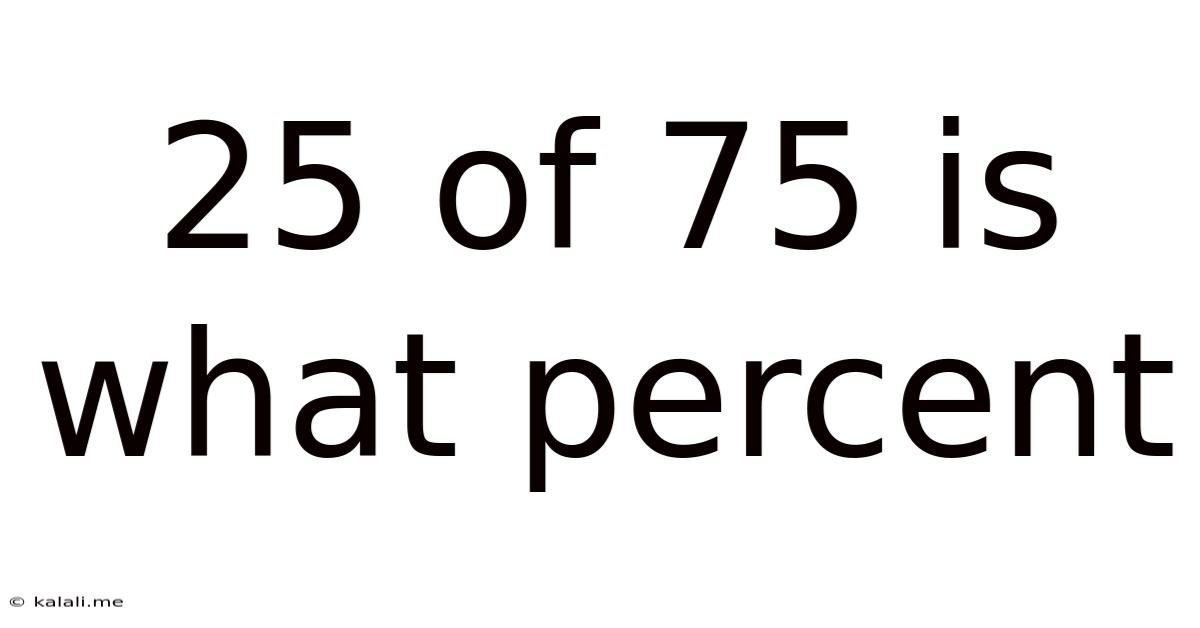
Table of Contents
25 out of 75 is What Percent? A Deep Dive into Percentage Calculations and Their Applications
Knowing how to calculate percentages is a fundamental skill with broad applications across various fields, from everyday budgeting to complex financial analysis. This article will not only answer the question "25 out of 75 is what percent?" but also explore the underlying concepts, different calculation methods, and practical examples illustrating the importance of percentage calculations. We’ll delve into the core mathematical principles, offer multiple approaches for solving percentage problems, and discuss how this seemingly simple calculation impacts diverse aspects of our lives.
Understanding Percentages: A Foundational Concept
A percentage is simply a fraction or ratio expressed as a number out of 100. The word "percent" itself comes from the Latin phrase "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100. For example, 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5.
This foundational understanding is crucial for tackling percentage calculations. It provides a framework for converting percentages to fractions and decimals and vice-versa, essential steps in many percentage problems. Mastering these conversions significantly simplifies more complex calculations.
Calculating "25 out of 75 is What Percent?"
Now, let's directly address the question: "25 out of 75 is what percent?". We can approach this problem using several methods.
Method 1: Using the Fraction Method
This is the most straightforward approach. We express the given numbers as a fraction and then convert the fraction into a percentage:
-
Form a fraction: Represent "25 out of 75" as the fraction 25/75.
-
Simplify the fraction: Both the numerator (25) and the denominator (75) are divisible by 25. Simplifying the fraction gives us 1/3.
-
Convert to a percentage: To convert the fraction 1/3 to a percentage, we divide the numerator (1) by the denominator (3) and then multiply the result by 100: (1 ÷ 3) × 100 ≈ 33.33%.
Therefore, 25 out of 75 is approximately 33.33%.
Method 2: Using the Decimal Method
This method involves converting the fraction to a decimal first and then to a percentage.
-
Form a fraction: As before, represent "25 out of 75" as the fraction 25/75.
-
Convert to a decimal: Divide the numerator (25) by the denominator (75): 25 ÷ 75 = 0.3333...
-
Convert to a percentage: Multiply the decimal by 100: 0.3333... × 100 ≈ 33.33%.
This method yields the same result as the fraction method, demonstrating the interchangeability of these approaches.
Method 3: Using Proportions
The proportion method is particularly useful when dealing with more complex percentage problems. It involves setting up a proportion where one ratio represents the given numbers and the other represents the unknown percentage.
-
Set up a proportion: We set up the proportion: 25/75 = x/100, where 'x' represents the unknown percentage.
-
Cross-multiply: Cross-multiplying gives us 75x = 2500.
-
Solve for x: Divide both sides by 75: x = 2500 ÷ 75 = 33.33...
Therefore, x ≈ 33.33%, confirming our previous results.
Practical Applications of Percentage Calculations
Percentage calculations are integral to numerous aspects of daily life and various professional fields. Here are some examples:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for managing personal finances effectively and making informed financial decisions. For example, calculating the interest on a loan or the discount on a sale item requires accurate percentage calculations. Similarly, analyzing investment performance involves comparing percentage changes in investment values.
-
Statistical Analysis: Percentages are fundamental to statistical analysis. They are used to represent proportions, frequencies, and rates in data sets. For example, expressing survey results, analyzing market share data, or presenting demographic information frequently involves percentages. Understanding these percentages helps in interpreting trends and drawing meaningful conclusions from data.
-
Scientific Research: Percentages are often used to express error margins, confidence intervals, and changes in experimental results. Scientific papers rely on accurate percentage calculations to present findings and conclusions reliably.
-
Business and Commerce: Calculating sales growth, market share, profit margins, and inventory turnover all involve percentages. Businesses use percentage analysis to track performance, identify areas for improvement, and make informed decisions about pricing, marketing, and resource allocation. For example, calculating year-over-year sales growth or comparing the market share of different competitors utilizes percentage analysis.
-
Everyday Life: We encounter percentages daily when calculating tips at restaurants, determining sale prices in stores, understanding nutritional information on food labels, or assessing the performance of sports teams. These everyday situations demonstrate the widespread applicability of percentage calculations.
Beyond the Basics: Advanced Percentage Calculations
While the calculation of "25 out of 75" is a relatively simple percentage problem, the concept of percentages extends to more complex scenarios. Here are some examples of advanced applications:
-
Percentage Increase/Decrease: These calculations determine the percentage change between two values. For example, calculating the percentage increase in sales from one year to the next or the percentage decrease in unemployment.
-
Percentage Points: It’s crucial to differentiate between percentage change and percentage points. For instance, if a company's market share increases from 10% to 15%, it's a 5 percentage point increase, but a 50% increase in market share.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest over time. This concept is crucial in understanding savings accounts, loans, and investments.
-
Percentage of a Percentage: This involves calculating a percentage of a value that is already a percentage. For example, calculating a discount on an item that is already on sale.
Conclusion: The Significance of Mastering Percentage Calculations
The seemingly simple calculation of "25 out of 75 is what percent?" highlights the importance of understanding and mastering percentage calculations. These calculations are fundamental to numerous aspects of life, from personal finance and statistical analysis to scientific research and business decision-making. By understanding the various methods of calculating percentages and their widespread applications, individuals can improve their problem-solving skills, make informed decisions, and confidently navigate a world filled with numerical data and proportional relationships. Whether you’re dealing with simple calculations or more complex scenarios, a solid grasp of percentages empowers you to interpret data accurately and effectively. Continuously practicing different percentage problems and exploring their diverse applications will strengthen your understanding and confidence in tackling these essential calculations.
Latest Posts
Latest Posts
-
What Is 1 Out Of 6 As A Percentage
Apr 18, 2025
-
How Many Inches Is 20 Meters
Apr 18, 2025
-
54 Is What Percent Of 60
Apr 18, 2025
-
What Is A Verbal Expression In Math
Apr 18, 2025
-
Does Liquid Have A Definite Volume
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 75 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.