27 4 As A Mixed Number
Kalali
Apr 27, 2025 · 4 min read
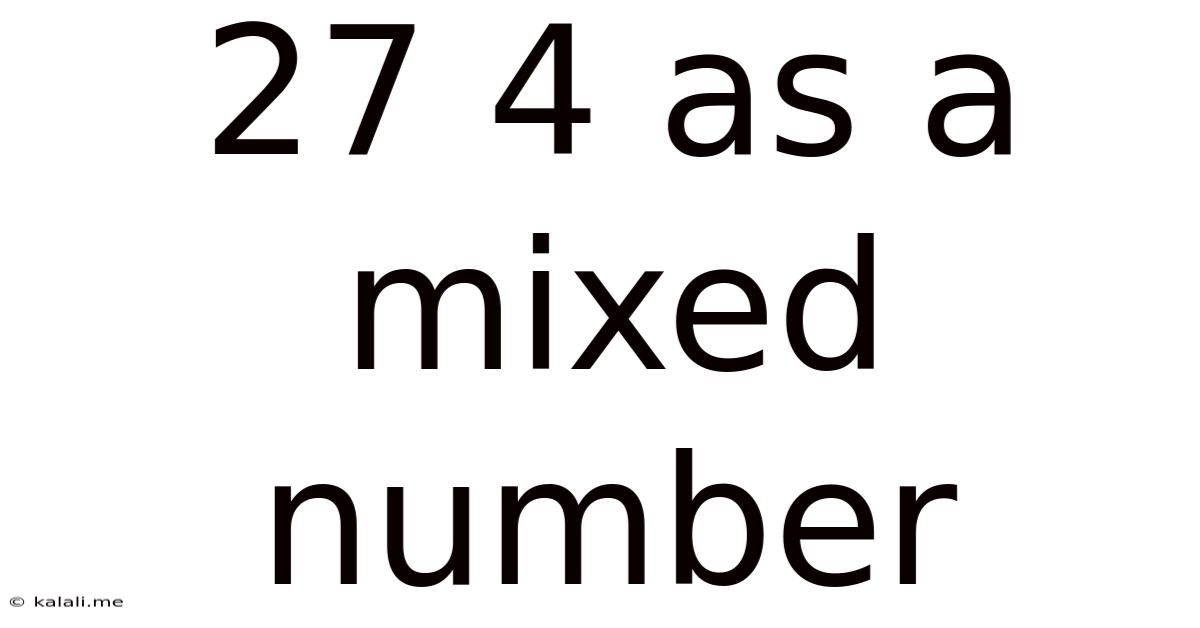
Table of Contents
Decoding 27/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their various representations is crucial in mathematics. This article delves deep into converting improper fractions, like 27/4, into mixed numbers. We'll explore the process step-by-step, provide practical examples, and offer additional insights to solidify your understanding. This comprehensive guide will equip you with the skills to confidently tackle similar fraction conversions.
What is a Mixed Number?
Before we dive into converting 27/4, let's define a mixed number. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). For example, 1 ¾, 2 ⅔, and 5 ⅛ are all mixed numbers. They represent quantities greater than one.
What is an Improper Fraction?
Conversely, an improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 5/4, 7/3, and, of course, our focus: 27/4. Improper fractions represent quantities greater than or equal to one. Converting improper fractions to mixed numbers makes them easier to visualize and understand in many contexts.
Converting 27/4 to a Mixed Number: The Step-by-Step Process
The conversion process involves dividing the numerator by the denominator. Here's how to convert 27/4:
-
Division: Divide the numerator (27) by the denominator (4).
27 ÷ 4 = 6 with a remainder of 3.
-
Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 6.
-
Numerator: The remainder (the number left over after the division) becomes the numerator of the fraction part of the mixed number. Here, the remainder is 3.
-
Denominator: The denominator of the mixed number remains the same as the denominator of the original improper fraction. So, the denominator stays 4.
-
Mixed Number: Combining the whole number and the fraction, we get the mixed number: 6 ¾.
Therefore, 27/4 expressed as a mixed number is 6 ¾.
Visualizing the Conversion
Imagine you have 27 identical items, and you want to divide them into groups of 4. You can make 6 complete groups of 4, leaving you with 3 items remaining. This remaining 3 items represent the fraction ¾ of another group of 4. This perfectly illustrates the mixed number 6 ¾.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in various real-world scenarios:
- Measurement: Imagine measuring the length of a piece of wood. You might measure it as 6 ¾ inches, which is more intuitive than 27/4 inches.
- Cooking: Recipes often call for mixed numbers in ingredient amounts, such as 2 ½ cups of flour or 1 ¼ teaspoons of baking powder.
- Construction: Construction projects often involve measurements expressed as mixed numbers for accuracy and ease of understanding.
Working with Mixed Numbers: Addition and Subtraction
Once you have converted an improper fraction to a mixed number, you can perform arithmetic operations more easily. Let's illustrate with addition and subtraction examples involving 6 ¾.
Example 1: Addition
Let's add 6 ¾ and 2 ⅛.
-
Convert to Improper Fractions: To add mixed numbers, it's often easier to first convert them back to improper fractions.
6 ¾ = (6 x 4 + 3) / 4 = 27/4 2 ⅛ = (2 x 8 + 1) / 8 = 17/8
-
Find a Common Denominator: To add fractions, they must have the same denominator. The least common multiple of 4 and 8 is 8.
27/4 = (27 x 2) / (4 x 2) = 54/8
-
Add the Fractions:
54/8 + 17/8 = 71/8
-
Convert Back to a Mixed Number:
71 ÷ 8 = 8 with a remainder of 7.
Therefore, 71/8 = 8 ⅞
Example 2: Subtraction
Let's subtract 1 ½ from 6 ¾.
-
Convert to Improper Fractions:
6 ¾ = 27/4 1 ½ = 3/2
-
Find a Common Denominator: The least common multiple of 4 and 2 is 4.
3/2 = (3 x 2) / (2 x 2) = 6/4
-
Subtract the Fractions:
27/4 - 6/4 = 21/4
-
Convert Back to a Mixed Number:
21 ÷ 4 = 5 with a remainder of 1.
Therefore, 21/4 = 5 ¼
Further Practice and Advanced Concepts
Mastering the conversion of improper fractions to mixed numbers requires practice. Try converting other improper fractions to mixed numbers. Explore different scenarios and work through addition and subtraction problems involving mixed numbers.
As you progress, you can explore more advanced concepts like:
- Multiplication and division of mixed numbers: These operations require a slightly more involved process, typically involving converting mixed numbers to improper fractions first.
- Comparing mixed numbers: Understanding how to compare the magnitude of different mixed numbers is essential for problem-solving.
- Working with mixed numbers in algebraic equations: Mixed numbers can appear in various algebraic expressions, requiring similar conversion and manipulation techniques.
By consistently practicing and exploring these concepts, you will develop a strong foundation in working with fractions and mixed numbers, enhancing your mathematical skills and problem-solving abilities. Remember, the key is to break down the process into manageable steps and understand the underlying principles. With dedication and practice, you’ll become proficient in handling all aspects of fraction manipulation. This includes converting between improper fractions and mixed numbers, performing arithmetic operations, and applying these skills to real-world problems.
Latest Posts
Latest Posts
-
How Many Cups Equals 2 Quarts
Apr 27, 2025
-
What Is 3 4 Ounces In Ml
Apr 27, 2025
-
How Many Ounces In One Cup Of Sour Cream
Apr 27, 2025
-
Median From Stem And Leaf Plot
Apr 27, 2025
-
How Many Inches Is 7 5 Ft
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 27 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.