28 Out Of 35 As A Percentage
Kalali
Mar 09, 2025 · 5 min read
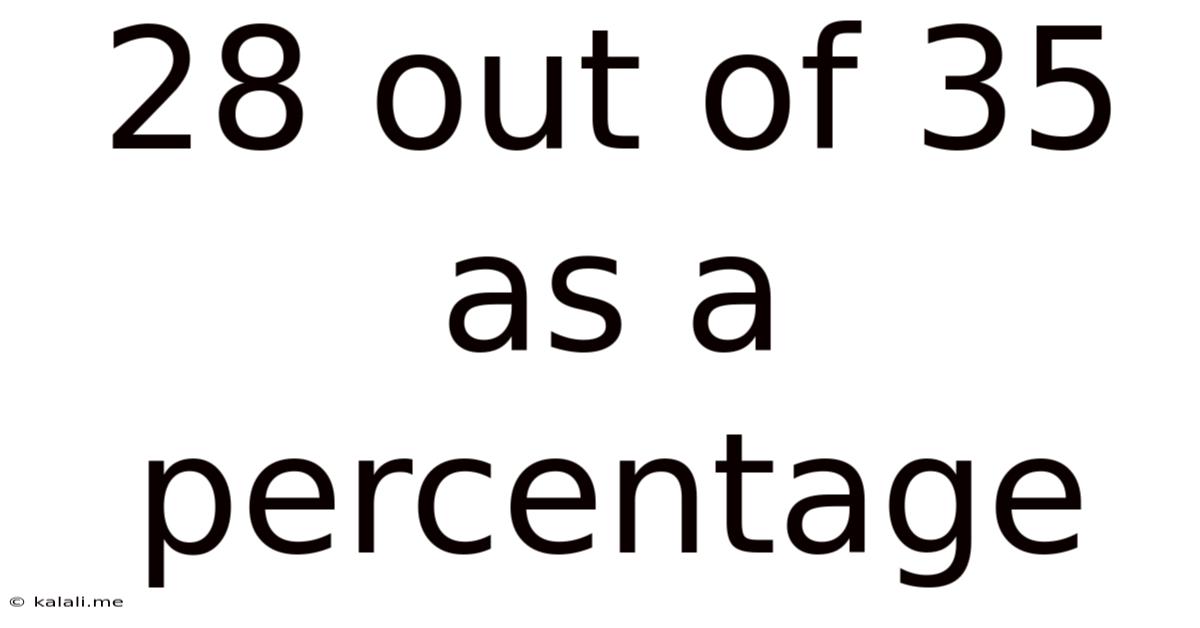
Table of Contents
28 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific research. Understanding how to convert fractions to percentages is crucial for effective data analysis and interpretation. This article provides a comprehensive guide on how to calculate 28 out of 35 as a percentage, explaining the process step-by-step and exploring various applications of percentage calculations. We'll also delve into the practical implications of understanding percentages and how this specific calculation relates to broader mathematical concepts.
Understanding the Basics of Percentages
Before we dive into the specific calculation of 28 out of 35 as a percentage, let's solidify our understanding of fundamental concepts. A percentage is simply a fraction expressed as a part of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be easily converted into a decimal or a fraction.
Converting Fractions to Percentages
The core principle of converting a fraction to a percentage lies in understanding the relationship between the fraction's parts and the whole. The general formula is:
(Part / Whole) * 100 = Percentage
In this formula:
- Part: Represents the numerator of the fraction (the number on top).
- Whole: Represents the denominator of the fraction (the number on the bottom).
By dividing the part by the whole and multiplying the result by 100, we obtain the equivalent percentage.
Calculating 28 out of 35 as a Percentage
Now, let's apply this formula to calculate 28 out of 35 as a percentage. In this case:
- Part = 28
- Whole = 35
Using the formula:
(28 / 35) * 100 = Percentage
-
Divide the part by the whole: 28 / 35 = 0.8
-
Multiply the result by 100: 0.8 * 100 = 80
Therefore, 28 out of 35 is equal to 80%.
Different Methods for Calculation
While the above method is the most straightforward, several other methods can be used to achieve the same result. These alternative methods can be particularly useful depending on the complexity of the fraction or the tools available.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 28/35. Both the numerator and the denominator share a common factor of 7. Simplifying gives us:
28 / 7 = 4 35 / 7 = 5
The simplified fraction becomes 4/5. Now, applying the formula:
(4 / 5) * 100 = 80%
This method can be advantageous when dealing with larger numbers, as simplifying the fraction can make the subsequent calculations easier.
Method 3: Using a Calculator
Calculators offer a quick and efficient way to convert fractions to percentages. Simply divide the numerator (28) by the denominator (35) and multiply the result by 100. Most calculators will automatically display the result as a percentage.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in many real-world scenarios. Here are a few examples illustrating the practical applications of percentage calculations, specifically highlighting the relevance of understanding that 28 out of 35 is 80%:
1. Academic Performance
Imagine a student scoring 28 out of 35 marks on a test. Knowing that this translates to 80% provides a clear indication of their performance. This percentage allows for easy comparison with other students' scores and helps determine the student's overall grade.
2. Business and Finance
In business, percentages are ubiquitous. For example, if a company sells 28 out of 35 products produced, they have an 80% sales rate. This metric provides valuable insight into sales performance, allowing businesses to analyze market demand, production efficiency, and overall profitability. Further analysis can be performed to identify reasons for the remaining 20% of unsold products.
3. Statistical Analysis
In statistical analysis, percentages are used extensively to represent proportions and probabilities. For instance, in a survey of 35 individuals, 28 responded positively to a particular question, indicating an 80% positive response rate. This information allows researchers to draw conclusions about the population's preferences or opinions.
4. Discount Calculations
Retailers frequently use percentages to advertise discounts. For example, an 80% discount on an item indicates a significant price reduction. Understanding percentage calculations allows consumers to easily determine the final price after the discount is applied.
Understanding the Remaining 20%
While 80% represents a significant portion, the remaining 20% (100% - 80%) is equally important to understand. In the context of the examples above, this 20% represents:
- In academic performance: The area where the student needs improvement.
- In business: Unsold products, potential lost revenue, areas needing attention in production or marketing.
- In statistical analysis: The segment of the population with a different perspective or opinion, requiring further investigation.
Understanding this 20% provides valuable insights and allows for targeted improvements or further investigation.
Advanced Applications: Percentage Increase and Decrease
The concept of percentages extends beyond simple fraction conversions. Understanding percentage increase and decrease is also crucial. For instance, if the number of positive responses increased from 28 to 31 out of 35, we would calculate the percentage increase. Similarly, a decrease from 28 to 25 would involve calculating a percentage decrease. These calculations help in tracking trends and making informed decisions based on dynamic data.
Conclusion: The Importance of Percentage Calculations
The ability to calculate percentages is a vital skill applicable across numerous disciplines. Understanding how to convert fractions to percentages, such as calculating 28 out of 35 as 80%, is essential for accurate data interpretation and effective decision-making in various contexts, from everyday life to complex professional applications. Mastering percentage calculations empowers individuals to better analyze data, interpret results, and make informed choices across a broad spectrum of fields. The ability to understand not just the 80% but also the crucial remaining 20% allows for a more comprehensive and nuanced understanding of the data at hand.
Latest Posts
Latest Posts
-
7am To 11pm Is How Many Hours
Jul 14, 2025
-
How Many Squares Of Shingles On A Pallet
Jul 14, 2025
-
What Is The Average Iq For 14 Year Old
Jul 14, 2025
-
Is Banana Pudding A Homo Or Heteronegous Mixture
Jul 14, 2025
-
What Year Were You Born In If You Are 15
Jul 14, 2025
Related Post
Thank you for visiting our website which covers about 28 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.