29 Is What Percent Of 20
Kalali
Apr 13, 2025 · 5 min read
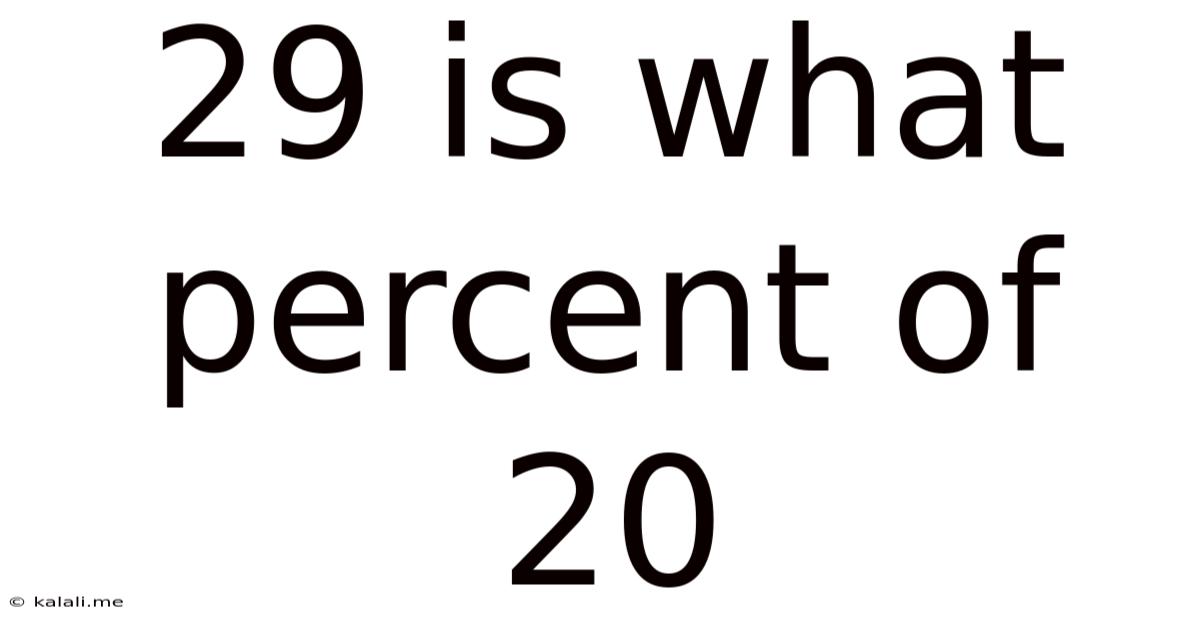
Table of Contents
29 is What Percent of 20? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "29 is what percent of 20?", opens the door to a fascinating exploration of percentage calculations, their underlying mathematical principles, and their wide-ranging applications in various fields. This article will not only answer the question directly but also delve into the methodology, explore different approaches to solving percentage problems, and illustrate the relevance of percentages in everyday life and professional contexts.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "29 is what percent of 20?". We explore various methods, real-world applications, and practical tips for mastering percentage calculations.
Understanding the Fundamentals of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. Understanding this basic concept is crucial for tackling any percentage problem.
Calculating "29 is What Percent of 20?" – Method 1: The Formula Approach
The most straightforward method involves using a basic percentage formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 29
- Whole: 20
Substituting these values into the formula, we get:
(29 / 20) * 100% = 145%
Therefore, 29 is 145% of 20. Notice that the result is greater than 100%, indicating that 29 is larger than 20.
Calculating "29 is What Percent of 20?" – Method 2: Proportion Method
Another effective approach involves setting up a proportion:
x / 100 = 29 / 20
Here, 'x' represents the percentage we need to find. To solve for 'x', we cross-multiply:
20x = 2900
Then, divide both sides by 20:
x = 145
Therefore, once again, we find that 29 is 145% of 20. This method reinforces the concept of equivalent ratios.
Understanding the Significance of the Result (145%)
The answer, 145%, highlights an important aspect of percentage calculations: percentages can exceed 100%. This occurs when the "part" is larger than the "whole." In our example, 29 is larger than 20, hence the percentage exceeds 100%. This is common in scenarios involving growth, increases, or comparisons where one value surpasses another.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life, including:
- Finance: Calculating interest rates, discounts, profit margins, tax rates, and investment returns. Understanding percentages is fundamental to making informed financial decisions. For instance, determining the percentage increase in your salary or the interest accrued on a loan depends heavily on accurate percentage calculations.
- Business: Analyzing sales figures, market share, growth rates, and cost-effectiveness. Businesses rely on percentage analysis to track performance, identify trends, and make strategic decisions. For example, calculating the percentage change in sales from one quarter to another is a key metric for business analysis.
- Science: Expressing experimental results, statistical data, and probabilities. Scientists use percentages to communicate findings concisely and compare different datasets. For example, expressing the percentage of a sample that exhibits a particular characteristic is commonplace in scientific reports.
- Everyday Life: Calculating tips, discounts, sales tax, and nutritional information on food labels. Daily encounters with percentages require quick and accurate mental or written calculations. For example, determining the final price of an item after a discount or the tip amount at a restaurant requires a sound understanding of percentage calculations.
- Education: Grading systems, test scores, and performance evaluations frequently use percentages to assess student progress and achievement. Understanding percentages is essential for students to track their academic progress effectively.
Advanced Percentage Calculations: Beyond the Basics
While the basic percentage formula covers many scenarios, more complex calculations might involve:
- Percentage Increase/Decrease: These calculations determine the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100%. A similar formula exists for percentage decrease. This is crucial in various contexts like tracking stock prices, population growth, or economic indicators.
- Finding the Whole from a Percentage: If you know a percentage and the part, you can calculate the whole. For example, if 25% of a number is 10, you can determine the original number using the formula: (Part / Percentage) * 100 = Whole.
- Percentage Points: It's important to distinguish between percentage points and percentages. A change of 5 percentage points is different from a 5% change. For instance, if a rate increases from 10% to 15%, it's a 5-percentage-point increase but a 50% increase relative to the original value.
Practical Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve various percentage problems to build your skills and confidence.
- Understand the Context: Pay close attention to the wording of the problem to ensure you're applying the correct formula.
- Use Visual Aids: Diagrams, charts, and graphs can help visualize percentage relationships and make calculations easier to understand.
- Utilize Calculators and Software: Calculators and spreadsheet software can simplify complex percentage calculations and save time.
- Break Down Complex Problems: Break down complex problems into smaller, manageable steps to avoid errors.
Conclusion: The Ubiquity and Importance of Percentages
The question "29 is what percent of 20?" may appear simple, but its answer – 145% – unlocks a deeper understanding of percentage calculations and their profound impact across diverse fields. Mastering percentage calculations is a valuable skill, enabling informed decisions in finance, business, science, and everyday life. By understanding the fundamental concepts, employing various calculation methods, and practicing regularly, one can confidently tackle even the most complex percentage problems. Remember, the ability to work with percentages effectively is a crucial asset in navigating the quantitative aspects of our world.
Latest Posts
Latest Posts
-
Cuanto Es 93 Grados Fahrenheit En Centigrados
Apr 13, 2025
-
How Do The Circulatory And Urinary Systems Work Together
Apr 13, 2025
-
How Many Cups Are In 32 Fluid Ounces
Apr 13, 2025
-
How Many Gallons In 45 Liters
Apr 13, 2025
-
How Many Cm In 26 Inches
Apr 13, 2025
Related Post
Thank you for visiting our website which covers about 29 Is What Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.