3 4 7 13 14 17 23
Kalali
Jul 12, 2025 · 5 min read
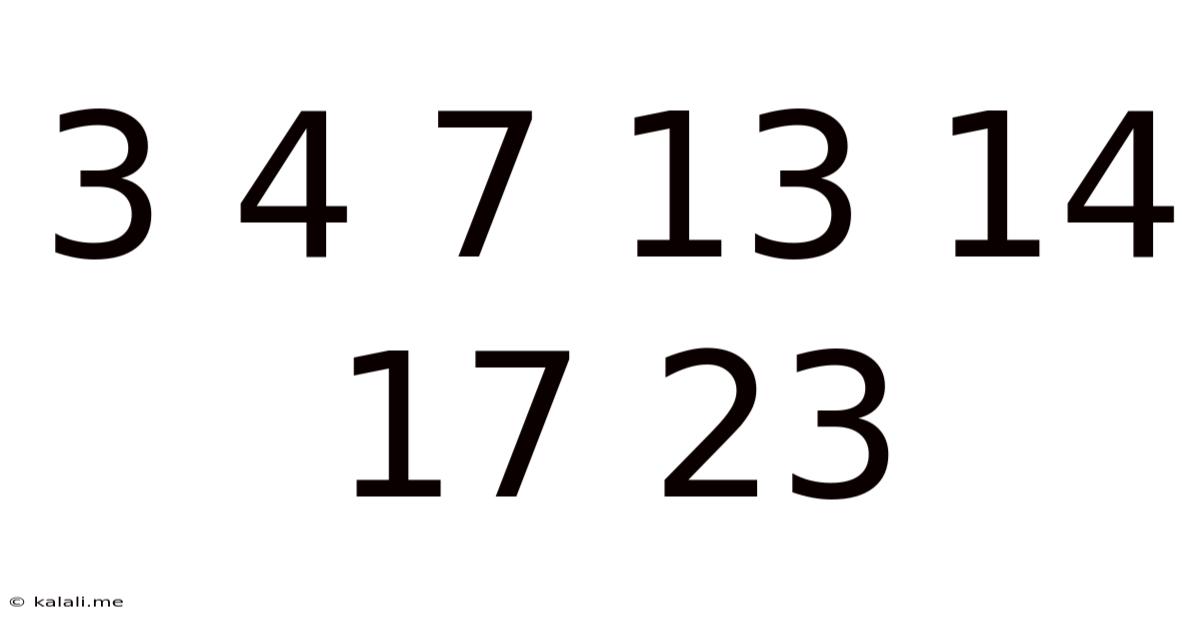
Table of Contents
Unraveling the Mystery: The Sequence 3, 4, 7, 13, 14, 17, 23 and Beyond
This seemingly random sequence of numbers – 3, 4, 7, 13, 14, 17, 23 – presents a fascinating puzzle. At first glance, it appears chaotic, defying easy pattern recognition. However, by applying various mathematical and logical approaches, we can uncover potential underlying structures, explore possible generating rules, and even predict future terms in the sequence. This article delves into different methods of analyzing this numerical puzzle, exploring the beauty and complexity hidden within seemingly random data. We will examine several possible explanations, highlighting the importance of considering multiple perspectives when dealing with number sequences. Understanding the techniques employed here can be valuable for anyone interested in mathematics, cryptography, or data analysis.
The Initial Assessment: A Lack of Obvious Patterns
Before embarking on sophisticated analyses, it's crucial to check for basic patterns. Simple arithmetic progressions (adding a constant value), geometric progressions (multiplying by a constant value), or even Fibonacci-like sequences (where each term is the sum of the preceding two) are often the first suspects. However, a quick examination reveals that none of these standard patterns fit our sequence. The differences between consecutive terms are erratic: 1, 3, 6, 1, 3, 6… This irregular pattern immediately suggests a more complex underlying structure. This lack of an immediately apparent solution highlights the need for a more nuanced approach.
Exploring Potential Generating Rules: A Multifaceted Approach
The absence of simple patterns necessitates a more creative approach. We can explore several potential avenues:
1. Modular Arithmetic and Prime Numbers:
Let's consider the prime factorization of each number in the sequence:
- 3: 3
- 4: 2²
- 7: 7
- 13: 13
- 14: 2 x 7
- 17: 17
- 23: 23
While no obvious pattern emerges directly from the prime factorization, we can explore relationships based on modular arithmetic. For example, we could examine the remainders when the numbers are divided by certain integers. This investigation could potentially reveal hidden periodicities or congruences. Exploring different moduli might uncover subtle relationships between the terms. However, a thorough examination reveals no consistent pattern through modular arithmetic with common moduli.
2. Difference Sequences and Recurrence Relations:
A common technique in sequence analysis is to examine the differences between consecutive terms. As mentioned earlier, the first difference sequence (1, 3, 6, 1, 3, 6) displays a pattern of repeating 1, 3, and 6. However, this repetition doesn't provide a reliable rule for predicting subsequent terms. We could also create a second difference sequence (2, 3, -5, 2, 3, -5…) which also repeats. The lack of a clear pattern in higher-order difference sequences suggests that a simple linear recurrence relation is unlikely. Exploring nonlinear recurrence relations, however, could be fruitful.
3. Combinations and Permutations:
It's possible the sequence is generated through a combination of smaller sequences or by applying permutations to a base set of numbers. This approach would require identifying potential subsets within the sequence and investigating their relationships. This might involve analyzing subsequences, like the prime numbers in the sequence (3, 7, 13, 17, 23) or the composite numbers (4, 14). Examining the possible permutations of these subsequences could offer insights.
4. Relationship to Other Mathematical Constants or Functions:
The sequence might be linked to other mathematical structures. We could explore relationships to:
- The prime numbers: As mentioned, the sequence contains several prime numbers. Exploring the distribution of primes might shed light on a hidden connection.
- Specific mathematical functions: Perhaps the sequence represents values of a particular function at integer inputs, or it could be related to a known mathematical constant through a specific transformation.
- Geometric patterns: It's worth checking for connections to geometric shapes, such as triangular numbers, square numbers, or other figurate numbers.
5. Statistical Analysis:
If no clear mathematical pattern is found, statistical methods can provide clues. We can analyze the distribution of the numbers, looking for statistical properties like mean, median, variance, and standard deviation. These statistical measures could point towards underlying probability distributions or other statistical regularities that might help explain the sequence's generation.
The Importance of Context and Potential External Factors
The analysis above focuses solely on the numbers themselves. However, the true origin of the sequence might lie outside the realm of pure mathematics. The sequence might represent:
- Coded information: The numbers could be part of a cipher or code, representing letters or symbols according to a specific key.
- Data from a real-world phenomenon: The sequence might represent measurements from a physical process or observation, in which case understanding the context is crucial.
- Part of a larger sequence: The given sequence might be only a small portion of a much longer, more complex sequence, and the underlying pattern might only become clear with more data.
Conclusion: The Ongoing Search for Patterns
The sequence 3, 4, 7, 13, 14, 17, 23 remains a fascinating enigma. While we have explored several potential avenues for understanding its underlying structure, none has yielded a definitive solution. The ambiguity highlights the complexity of pattern recognition and the importance of considering multiple perspectives. The quest to unravel the sequence's mystery continues, encouraging further exploration and the application of diverse mathematical and logical techniques. The challenge underscores the captivating nature of mathematical puzzles and the enduring human fascination with deciphering hidden patterns within seemingly random data. Further investigation might involve the use of advanced computational methods, exploring the sequence's behavior across various mathematical domains. This exploration could lead to the discovery of unforeseen connections and a deeper understanding of the mathematical principles that govern such seemingly random sequences. The process itself, however, remains just as valuable as any potential solution found, teaching valuable lessons in analytical thinking and problem-solving.
Latest Posts
Latest Posts
-
115 Out Of 150 As A Percentage
Jul 12, 2025
-
How Many Cups Is 8 Ounces Of Dry Macaroni
Jul 12, 2025
-
What Do You Call A Group Of Deer
Jul 12, 2025
-
How Do I Delete My Manhunt Account
Jul 12, 2025
-
How Much Does A Dump Truck Weigh
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about 3 4 7 13 14 17 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.