3 4 Divided By 1 1 2
Kalali
Jul 04, 2025 · 5 min read
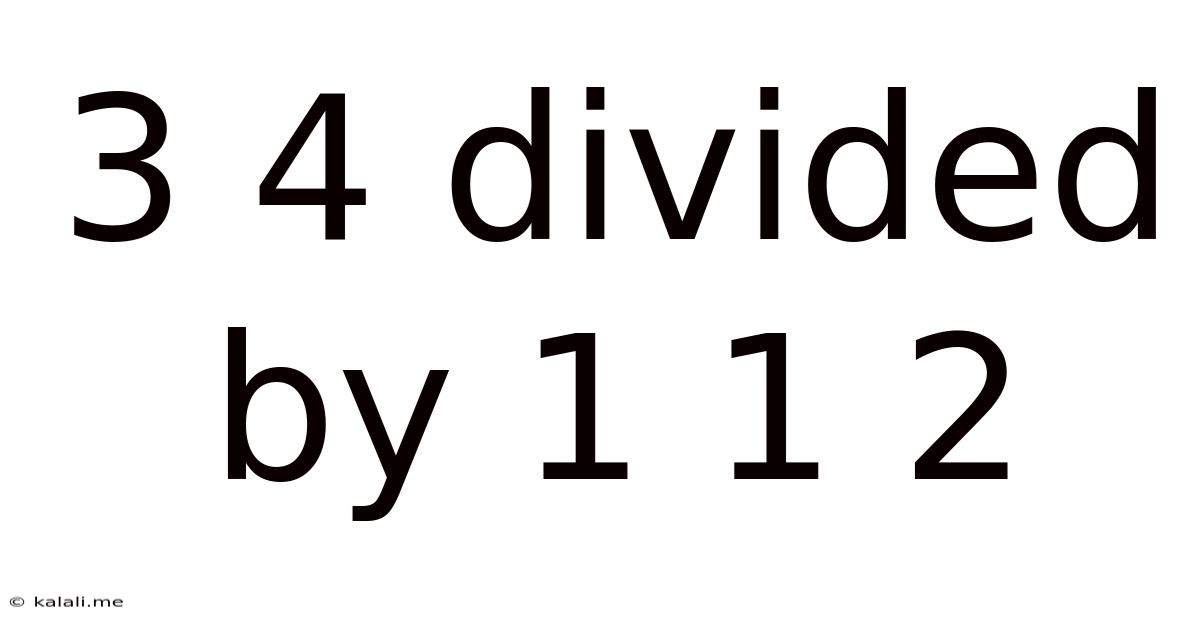
Table of Contents
Deconstructing the Division: 3 4/11 Divided by 1 1/2
This article will comprehensively explore the solution to the mathematical problem: 3 4/11 divided by 1 1/2. We'll move beyond simply providing the answer and delve into the underlying principles, exploring different methods for solving mixed number division, and highlighting practical applications. Understanding mixed number division is crucial for various fields, including cooking, construction, and engineering, where precise measurements and calculations are paramount. By the end of this article, you'll not only know the answer but also possess a solid grasp of the methodology involved.
Understanding Mixed Numbers and Their Importance
Before we tackle the division problem, let's review mixed numbers. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our problem, 3 4/11 and 1 1/2 are mixed numbers. Understanding how to work with mixed numbers is essential in many real-world scenarios. Imagine you're following a recipe that calls for 2 1/4 cups of flour. You need to be able to understand and work with that mixed number to successfully bake your cake. Similarly, in construction, precise measurements involving mixed numbers are crucial for accurate building and avoiding errors.
Method 1: Converting to Improper Fractions
The most common and often the most efficient method for dividing mixed numbers is to first convert them into improper fractions. An improper fraction has a numerator that is larger than or equal to its denominator.
-
Converting 3 4/11 to an improper fraction: Multiply the whole number (3) by the denominator (11), add the numerator (4), and place the result over the original denominator. This gives us (3 * 11) + 4 / 11 = 37/11.
-
Converting 1 1/2 to an improper fraction: Following the same process, we get (1 * 2) + 1 / 2 = 3/2.
Now our problem becomes: 37/11 ÷ 3/2.
Dividing fractions involves inverting the second fraction (the divisor) and multiplying. So we have:
37/11 * 2/3 = (37 * 2) / (11 * 3) = 74/33
This improper fraction can be converted back into a mixed number by dividing the numerator (74) by the denominator (33). 74 divided by 33 is 2 with a remainder of 8. Therefore, the answer is 2 8/33.
Method 2: Long Division with Mixed Numbers (A More Complex Approach)
While converting to improper fractions is generally preferred, it's also possible to perform long division directly with mixed numbers. This method is more complex and prone to errors, but understanding it can provide a deeper insight into the process.
This method involves a step-by-step approach:
-
Estimate: Begin by estimating the answer. 3 4/11 is a little more than 3, and 1 1/2 is 1.5. Dividing 3 by 1.5 gives 2, suggesting our answer should be around 2.
-
Convert to decimals (optional): While not strictly necessary, converting the mixed numbers to decimals can simplify the initial steps. 3 4/11 ≈ 3.36 and 1 1/2 = 1.5. Dividing 3.36 by 1.5 gives approximately 2.24. This provides a useful check on our final answer.
-
Long division with mixed numbers: This approach is significantly more challenging and involves multiple steps of converting remainders and working with fractions, making it less efficient than the improper fraction method. We'll skip the detailed steps here due to complexity and the superior efficiency of the improper fraction method. The process would involve repeatedly subtracting the divisor (1 1/2) from the dividend (3 4/11) and keeping track of the remainder until the remainder is less than the divisor. This method is generally less practical and more error-prone.
Real-World Applications and Examples
The ability to divide mixed numbers is vital in several everyday contexts:
-
Cooking: A recipe calls for 5 1/2 cups of flour, but you only want to make half the recipe. You would need to divide 5 1/2 by 2 to determine the amount of flour needed.
-
Construction: A carpenter needs to divide a 12 3/4-foot board into 3 equal pieces. Dividing 12 3/4 by 3 will give the length of each piece.
-
Sewing: If you need to cut 2 1/3 yards of fabric from a 5 2/3 yard roll, dividing 5 2/3 by 2 1/3 will tell you how many pieces you can cut.
-
Finance: If you're splitting a bill of $25 1/2 among three people, you'd need to divide the amount by 3 to calculate each person's share.
Addressing Potential Errors and Troubleshooting
When working with mixed numbers, common errors include:
-
Incorrect conversion to improper fractions: Double-check your calculations when converting mixed numbers to improper fractions to avoid errors that propagate through the rest of your calculations.
-
Mistakes in fraction multiplication/division: Remember the rule for dividing fractions: invert the second fraction and multiply. Carefully perform the multiplication of numerators and denominators.
-
Improper simplification: Always simplify your final answer to its lowest terms. For example, 74/33 can be simplified to 2 8/33.
Further Exploration and Practice
To solidify your understanding, consider practicing more division problems with mixed numbers. Try varying the complexity of the numbers involved. Online resources and textbooks offer numerous practice problems. The more you practice, the more comfortable and accurate you'll become with this essential mathematical skill. Consider exploring problems with larger mixed numbers or those involving more complex fractions. This added challenge will strengthen your understanding and improve your problem-solving skills.
Conclusion: Mastering Mixed Number Division
Dividing mixed numbers is a fundamental skill with broad applications. While it may seem daunting at first, mastering this concept significantly enhances your mathematical abilities and problem-solving skills. By understanding the process of converting to improper fractions and then performing the division, you can confidently tackle any mixed number division problem you encounter. Remember to check your work carefully and practice regularly to ensure accuracy and build your confidence. With practice and a clear understanding of the underlying principles, this seemingly complex operation becomes straightforward and manageable. This method ensures accuracy and provides a more efficient and less error-prone solution compared to attempting long division directly with mixed numbers. The ability to confidently work with mixed numbers is a valuable asset in various aspects of life, from everyday tasks to more complex professional applications.
Latest Posts
Latest Posts
-
What Elements Are Most Likey To Becom Anions
Jul 31, 2025
-
How Old Is Someone Born In 1937
Jul 31, 2025
-
How Many Times Is But God In The Bible
Jul 31, 2025
-
Why Did The Scientists Stay At The Math Teachers House
Jul 31, 2025
-
How Many Laps Is 500 Yards In A Pool
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.