3 Is What Percent Of 24
Kalali
Apr 15, 2025 · 6 min read
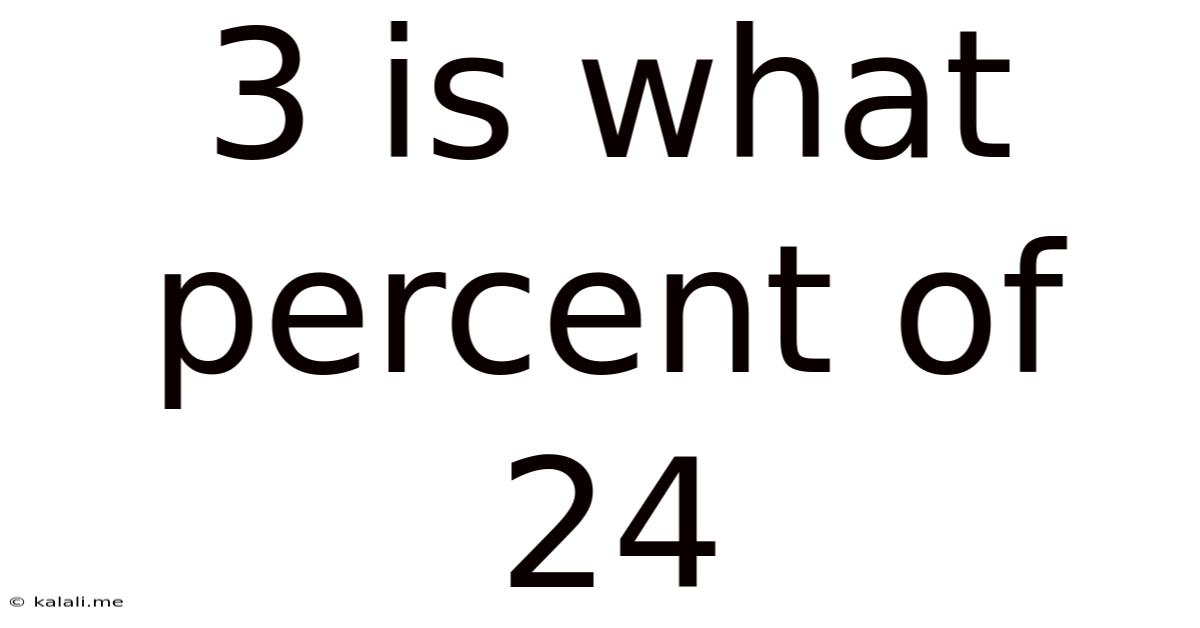
Table of Contents
3 is What Percent of 24? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "3 is what percent of 24?", opens the door to a vast world of percentage calculations and their practical applications across numerous fields. Understanding percentages is crucial for everything from calculating discounts and taxes to analyzing financial statements and understanding statistical data. This article will not only answer the initial question but also explore the underlying concepts, provide multiple methods for solving similar problems, and delve into real-world examples where percentage calculations are indispensable.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "3 is what percent of 24?". This guide covers various methods, real-world applications, and tips for mastering percentage calculations.
Understanding Percentages: The Basics
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 10% means 10 out of 100, which can also be expressed as the fraction 10/100 or the decimal 0.10.
Understanding this fundamental concept is critical for tackling percentage problems. The core relationship is:
Part / Whole = Percentage / 100
This formula forms the basis for solving various percentage problems, regardless of whether you're trying to find the percentage, the part, or the whole.
Method 1: Using the Percentage Formula Directly
Let's apply the fundamental formula to solve "3 is what percent of 24?":
- Part: 3
- Whole: 24
- Percentage: This is what we need to find (let's represent it as 'x')
Substituting these values into the formula:
3 / 24 = x / 100
To solve for x, we cross-multiply:
3 * 100 = 24 * x
300 = 24x
x = 300 / 24
x = 12.5
Therefore, 3 is 12.5% of 24.
Method 2: Converting to a Decimal and Multiplying by 100
Another approach involves first calculating the decimal equivalent of the fraction representing the part and the whole, and then multiplying by 100 to convert it to a percentage.
- Form the fraction: 3/24
- Convert to a decimal: 3 divided by 24 equals 0.125
- Multiply by 100 to get the percentage: 0.125 * 100 = 12.5%
This method provides a straightforward and intuitive way to calculate percentages, particularly when using a calculator.
Method 3: Using Proportions
This method relies on setting up a proportion to solve the problem. A proportion is a statement that two ratios are equal. We can set up the proportion as follows:
3/24 = x/100
Cross-multiplying gives:
24x = 300
x = 300/24 = 12.5
Again, we arrive at the answer: 3 is 12.5% of 24.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and professional settings. Here are a few examples:
- Sales and Discounts: Calculating discounts offered during sales events. For instance, a 20% discount on a $100 item means a $20 discount ($100 * 0.20 = $20).
- Taxes: Determining the amount of sales tax or income tax owed. A 6% sales tax on a $50 purchase translates to a $3 tax ($50 * 0.06 = $3).
- Financial Analysis: Analyzing financial statements like income statements and balance sheets. Percentage changes in revenue, expenses, or profits help understand trends and performance. For example, comparing the percentage change in sales year-over-year is essential for business evaluation.
- Statistics and Data Analysis: Percentages are crucial for representing and interpreting data. For instance, expressing survey results as percentages makes it easier to understand the proportion of respondents who hold a particular viewpoint. This includes calculating percentages of market share, customer satisfaction, and various other metrics.
- Scientific Research: In scientific research, percentages are commonly used to express experimental results, error margins, and to present data clearly in graphs and charts. This includes determining success rates, probability, and experimental yields.
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans. A 5% interest rate on a $1000 investment yields $50 interest in a year ($1000 * 0.05 = $50). Understanding compound interest also relies heavily on percentage calculations.
- Tip Calculation: Determining the appropriate tip amount in a restaurant. A 15% tip on a $50 bill amounts to $7.50 ($50 * 0.15 = $7.50).
- Grade Calculation: Converting test scores or assignments to percentages for calculating a final grade. If a student scores 18 out of 20 on a test, their score is 90% (18/20 * 100 = 90%).
Solving More Complex Percentage Problems
While the initial problem was straightforward, percentage problems can become more complex. Here are a few scenarios and how to approach them:
- Finding the Whole: If you know the percentage and the part, you can find the whole. For example, "15% of what number is 6?" Set up the equation: 0.15 * x = 6, solving for x gives x = 40.
- Finding the Part: If you know the percentage and the whole, you can find the part. For example, "What is 25% of 80?" The calculation is 0.25 * 80 = 20.
- Percentage Increase/Decrease: Calculating percentage changes over time. This involves finding the difference between two values, dividing the difference by the original value, and then multiplying by 100. For example, if sales increased from $100 to $120, the percentage increase is: (($120-$100)/$100) * 100 = 20%.
- Compound Percentage Changes: When dealing with multiple percentage changes applied sequentially, the calculations become more intricate. You must apply each percentage change one after another rather than simply adding them together.
Tips for Mastering Percentage Calculations
- Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve various problems of increasing complexity.
- Use a Calculator: Utilize a calculator for complex problems or for efficiency.
- Understand the Underlying Concepts: Focus on understanding the fundamental relationship between parts, wholes, and percentages.
- Break Down Complex Problems: Decompose complex problems into simpler steps to make them more manageable.
- Check Your Answers: Always verify your answers using alternative methods or by estimating the result. A quick estimate can help identify significant errors in calculation.
Conclusion
The seemingly simple question, "3 is what percent of 24?", serves as an excellent springboard to explore the world of percentage calculations. Understanding percentages is a fundamental skill with widespread applications in diverse fields. By mastering the different methods presented here and practicing regularly, you'll develop the confidence and proficiency to tackle any percentage problem, no matter its complexity. The ability to perform accurate percentage calculations is a valuable asset, whether in personal finance, professional endeavors, or academic pursuits. Remember the core formula and practice regularly – you'll soon find yourself effortlessly navigating the world of percentages.
Latest Posts
Latest Posts
-
How Many Cups In A Bag Of Chocolate Chips
Jul 05, 2025
-
Spyware Can Result In All Of The Following Except
Jul 05, 2025
-
What Year Were 16 Year Olds Born
Jul 05, 2025
-
Two Letter Symbol From The Periodic Table
Jul 05, 2025
-
How Long Will It Take To Walk 5 Miles
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.