3 Is What Percent Of 30
Kalali
Apr 25, 2025 · 5 min read
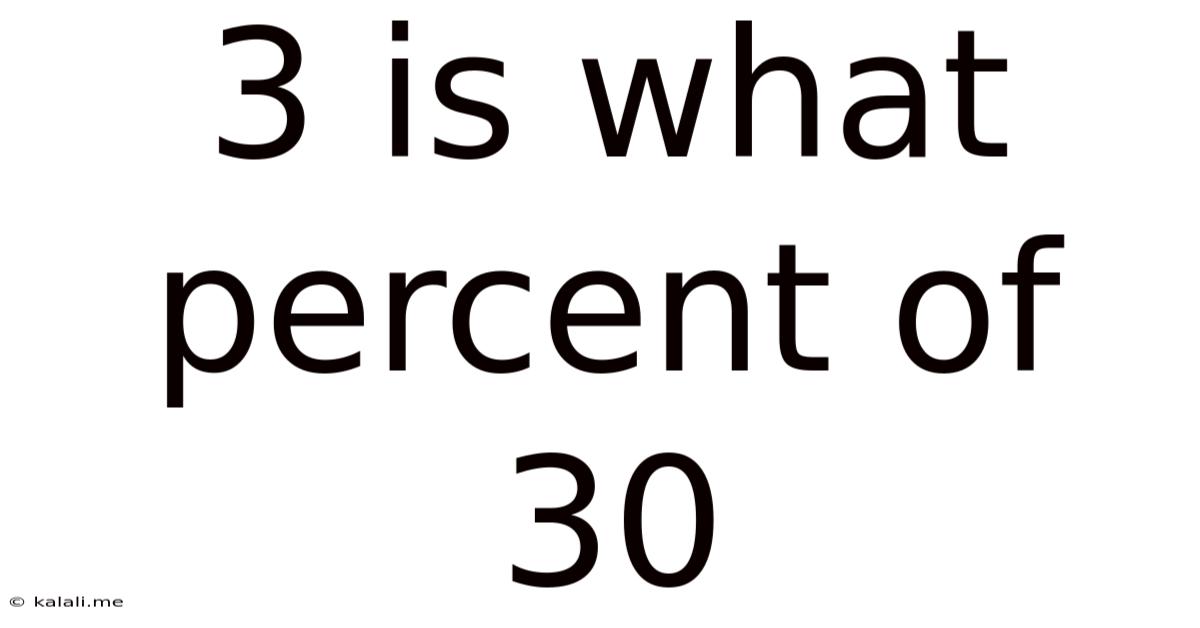
Table of Contents
3 is What Percent of 30? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "3 is what percent of 30?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation unlocks a powerful tool applicable across numerous fields. This article provides a comprehensive guide, delving beyond the basic calculation to explore real-world applications and advanced percentage concepts.
Meta Description: Learn how to calculate percentages, understand the concept of "3 is what percent of 30," explore real-world applications, and discover advanced percentage techniques. This comprehensive guide covers everything from basic arithmetic to complex percentage problems.
Understanding Percentages: The Foundation
Percentages are essentially fractions expressed as parts of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a ratio, comparing a portion to a whole, scaled to a base of 100. This standardized representation makes it easy to compare different ratios and understand proportions.
For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is crucial for tackling any percentage problem, including our central question: "3 is what percent of 30?"
Calculating "3 is What Percent of 30?"
To solve this, we can use a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 3
- Whole: 30
Substituting these values into the formula:
(3 / 30) * 100 = 10%
Therefore, 3 is 10% of 30.
Different Approaches to the Calculation
While the above method is the most straightforward, several other approaches can yield the same result. These alternative methods offer a deeper understanding of the underlying mathematical concepts and can be particularly useful when dealing with more complex percentage problems.
-
Using Proportions: We can set up a proportion: 3/30 = x/100. Solving for x (the percentage) gives us x = 10.
-
Decimal Conversion: First, convert the fraction 3/30 to a decimal (0.1). Then, multiply the decimal by 100 to express it as a percentage (0.1 * 100 = 10%).
-
Using a Calculator: Most calculators have a percentage function that simplifies the calculation. Simply enter 3 ÷ 30 × 100 to get the answer directly.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable across various fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage change is crucial for analyzing financial performance and making informed investment decisions. For example, determining the percentage increase or decrease in sales revenue year-over-year is a fundamental aspect of financial analysis.
-
Sales and Marketing: Discount percentages, conversion rates (the percentage of website visitors who make a purchase), and market share are all expressed and calculated using percentages. Marketing campaigns often focus on improving conversion rates and increasing market share, both measured as percentages.
-
Science and Research: Percentages are used to represent statistical data, experimental results, and error margins. For instance, expressing the percentage of a population with a particular characteristic or the percentage of successful outcomes in a scientific experiment.
-
Everyday Life: Calculating tips, understanding sale prices, figuring out discounts, and even calculating cooking ingredient proportions often involve percentage calculations.
Advanced Percentage Concepts
Beyond the basic calculation, several advanced concepts build upon the fundamental principles of percentages:
-
Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100. This is used to track changes in various metrics like sales, prices, and population.
-
Percentage Point Difference: This is the arithmetic difference between two percentages. It's crucial to distinguish this from percentage change. For example, a change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
-
Compounding Percentages: This involves applying a percentage change repeatedly over time. It's particularly relevant in finance, where interest compounds over periods. Understanding compounding is critical for long-term financial planning.
-
Percentage of a Percentage: This involves finding a percentage of a percentage, often encountered in multi-step calculations. For instance, calculating a discount on an already discounted price involves this concept.
Troubleshooting Common Percentage Problems
Many common errors arise when working with percentages. Here are some crucial points to remember:
-
Clarifying the Whole: Always identify the correct whole or base value before performing any calculations. The whole is the number to which the percentage refers.
-
Distinguishing Percentage Change and Percentage Point Difference: Remember the difference and use the appropriate calculation method.
-
Avoiding Common Errors with Compound Percentages: Ensure that you correctly apply the percentage change repeatedly in the right order, especially when dealing with multiple compounding periods.
-
Checking your work: Use different methods to solve the same problem to ensure accuracy. Verify the results logically – does your answer make sense in the context of the problem?
Expanding Your Percentage Skills
To enhance your understanding and proficiency with percentage calculations, consider the following resources and practices:
-
Practice Regularly: The more you practice, the better you'll become at solving various percentage problems. Work through a variety of problems from simple to complex.
-
Use Online Calculators and Tools: Many online calculators and tools can help you check your work and understand the steps involved in solving complex percentage problems.
-
Explore More Advanced Concepts: Dive deeper into percentage change, compounding percentages, and other advanced concepts to expand your knowledge.
-
Relate Percentages to Real-World Situations: Apply your knowledge to real-world problems to enhance understanding and retention. This makes learning more meaningful and engaging.
By understanding the fundamentals, mastering the calculation techniques, and exploring advanced applications, you can leverage the power of percentages in countless situations—both personally and professionally. The seemingly simple question, "3 is what percent of 30?" serves as an excellent gateway to this powerful and versatile mathematical tool.
Latest Posts
Latest Posts
-
What Percent Of 9 Is 4
Apr 25, 2025
-
What Is The Blending Theory Of Inheritance
Apr 25, 2025
-
Cuanto Es 135 Cm En Pulgadas
Apr 25, 2025
-
How Many Cups Is 8 Quarts Of Water
Apr 25, 2025
-
How Much Is 48 Fl Oz
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.