3 Is What Percent Of 8
Kalali
Mar 30, 2025 · 5 min read
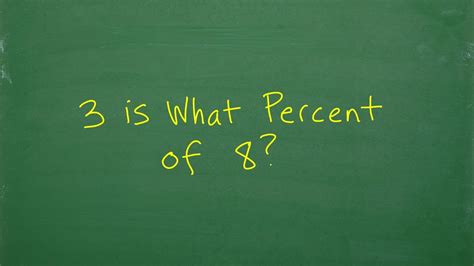
Table of Contents
3 is What Percent of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the question, "3 is what percent of 8?", providing a step-by-step solution, exploring different calculation methods, and showcasing real-world applications. We'll also examine related concepts and provide you with the tools to confidently solve similar percentage problems.
Understanding Percentages: The Basics
Before tackling the specific problem, let's clarify the core concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2.
Key Terms:
- Percentage: The portion of a whole expressed as a number out of 100.
- Part: The smaller amount being compared to the whole.
- Whole: The total amount.
Calculating "3 is What Percent of 8?" - Method 1: The Formula Approach
The most direct way to solve this problem is using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part = 3
- Whole = 8
Substituting these values into the formula:
(3 / 8) * 100 = 37.5%
Therefore, 3 is 37.5% of 8.
Calculating "3 is What Percent of 8?" - Method 2: Using Proportions
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
3/8 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
3 * 100 = 8 * x
300 = 8x
x = 300 / 8
x = 37.5
Again, this confirms that 3 is 37.5% of 8.
Visualizing the Percentage: A Pie Chart Representation
To further illustrate the concept, let's visualize this using a pie chart. Imagine a pie representing the whole (8). One slice represents the part (3). The percentage (37.5%) indicates the size of that slice relative to the entire pie. This visual representation reinforces the understanding of the relationship between the part, the whole, and the percentage.
!
Real-World Applications: Putting Percentages to Work
Understanding percentage calculations is crucial in many everyday situations:
1. Discounts and Sales:
Imagine a shirt originally priced at $8 is on sale for $3. Using the methods outlined above, we've already established that the discount is 37.5%. This type of calculation is vital for quickly assessing the value of a sale.
2. Tax Calculations:
If a sales tax is 8% and an item costs $3, the tax amount would be (8/100) * $3 = $0.24. This shows how percentages are used to determine the tax amount added to the original price.
3. Grade Calculations:
In education, percentages are commonly used to express grades. If a student scores 3 out of 8 points on a quiz, their score is 37.5%. This helps to standardize and compare student performance.
4. Data Analysis:
Percentages are fundamental in data analysis. For instance, if a survey shows that 3 out of 8 respondents prefer a particular product, the percentage of respondents favoring that product is 37.5%. This aids in interpreting and presenting survey results.
5. Financial Calculations:
In finance, percentage changes are used to track investment growth or loss. If an investment worth $8 increased by $3, it has grown by 37.5%. This allows for a clear understanding of investment performance.
Expanding on Percentage Calculations: Related Concepts
The calculation of "3 is what percent of 8?" is a foundational step in understanding more complex percentage problems. Let's explore some related concepts:
1. Finding the Whole:
If we know the percentage and the part, we can find the whole. For example: If 37.5% of a number is 3, what is the number?
The formula to solve this is:
Whole = (Part / Percentage) * 100
Whole = (3 / 37.5) * 100 = 8
2. Finding the Part:
If we know the percentage and the whole, we can find the part. For example: What is 37.5% of 8?
The formula is:
Part = (Percentage / 100) * Whole
Part = (37.5 / 100) * 8 = 3
3. Percentage Increase/Decrease:
Calculating percentage increase or decrease involves finding the difference between two values and expressing that difference as a percentage of the original value.
For example, if a value increases from 5 to 8, the percentage increase is:
((8 - 5) / 5) * 100 = 60%
Similarly, if a value decreases from 8 to 5, the percentage decrease is:
((8 - 5) / 8) * 100 = 37.5%
Mastering Percentages: Tips and Tricks
- Practice Regularly: The more you practice solving percentage problems, the more comfortable and efficient you'll become.
- Use a Calculator: For more complex problems, a calculator can save time and increase accuracy.
- Understand the Concepts: Don't just memorize formulas; understand the underlying principles.
- Visualize: Use diagrams, charts, or other visual aids to help you grasp the concepts.
- Break Down Complex Problems: Divide complex percentage problems into smaller, more manageable steps.
Conclusion: The Power of Percentages
The seemingly simple question, "3 is what percent of 8?" opens the door to a vast understanding of percentage calculations. From everyday shopping to complex financial analysis, the ability to accurately and confidently work with percentages is a valuable asset. By mastering the methods, visualizing the concepts, and practicing regularly, you can build a strong foundation in this essential mathematical skill. Remember, the power of percentages lies in their ability to transform complex ratios and fractions into easily understandable and comparable figures.
Latest Posts
Latest Posts
-
48 Oz Equals How Many Cups
Apr 01, 2025
-
What Is 8 20 As A Percentage
Apr 01, 2025
-
40 Is 80 Percent Of What Number
Apr 01, 2025
-
48 Of 60 Is What Percent
Apr 01, 2025
-
How Many Gallons Is 7 Litres
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
