3 Is What Percentage Of 18
Kalali
Apr 27, 2025 · 5 min read
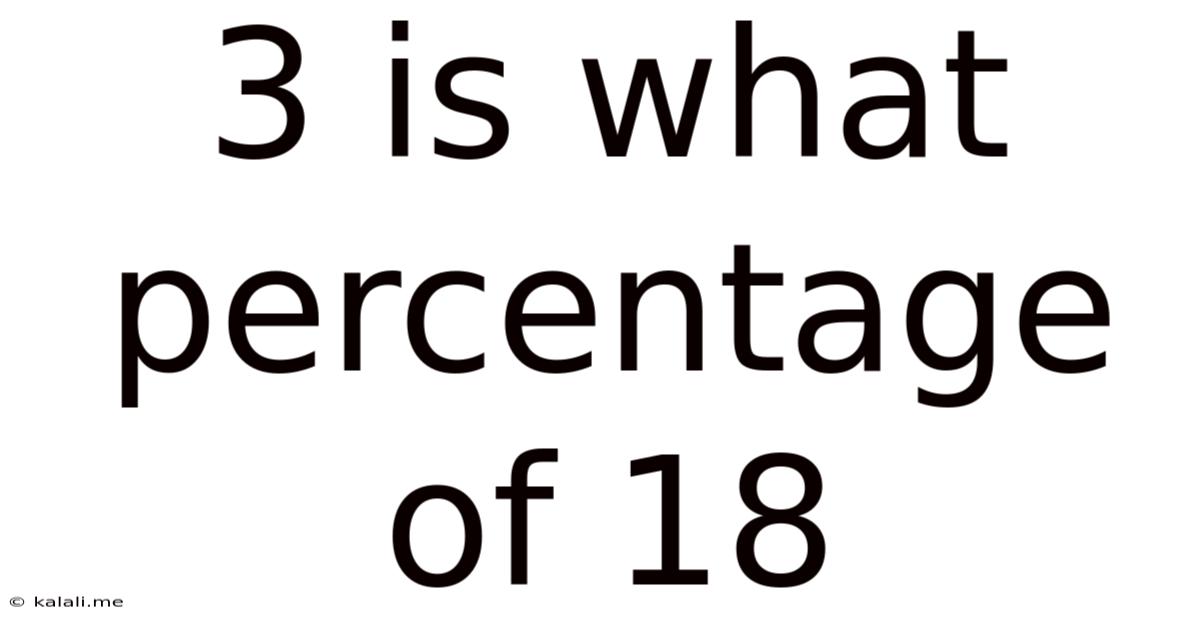
Table of Contents
3 is What Percentage of 18? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "3 is what percentage of 18?", opens the door to a fascinating exploration of percentages, their mathematical underpinnings, and their widespread applications in various fields. Understanding percentages is fundamental to numerous aspects of life, from calculating discounts and taxes to analyzing financial data and interpreting statistical information. This article will not only answer the initial question but also provide a comprehensive understanding of percentage calculations, their practical uses, and some advanced concepts.
Meta Description: Learn how to calculate percentages with a step-by-step guide solving "3 is what percentage of 18?". Discover practical applications of percentages in finance, statistics, and everyday life, including advanced percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fundamental concept is the cornerstone of all percentage calculations.
To calculate a percentage, we use a simple formula:
(Part / Whole) * 100 = Percentage
In our example, "3 is what percentage of 18?", we identify:
- Part: 3
- Whole: 18
Now, let's plug these values into the formula:
(3 / 18) * 100 = 16.67%
Therefore, 3 is 16.67% of 18.
Step-by-Step Calculation: A Detailed Breakdown
Let's break down the calculation process further to ensure a clear understanding:
-
Divide the Part by the Whole: The first step is to divide the "part" (3) by the "whole" (18). This gives us a decimal value: 3 ÷ 18 = 0.166666...
-
Multiply by 100: To convert this decimal to a percentage, multiply the result by 100. This shifts the decimal point two places to the right: 0.166666... * 100 = 16.6666...%
-
Round to the Desired Precision: Depending on the context, you may need to round the percentage to a specific number of decimal places. In most cases, rounding to two decimal places (16.67%) is sufficient. However, in situations requiring higher accuracy, you may need more decimal places.
Practical Applications of Percentages
Percentages are ubiquitous in various aspects of daily life and professional settings. Here are some examples:
-
Finance: Calculating interest rates on loans and savings accounts, understanding profit margins, analyzing investment returns, and determining discounts and sales tax. For example, a 20% discount on a $100 item means you save $20.
-
Statistics: Representing data in charts and graphs, calculating probabilities, and analyzing survey results. Percentages help visualize and interpret data more effectively.
-
Science: Expressing concentrations of solutions, measuring error rates in experiments, and analyzing statistical significance in research.
-
Everyday Life: Calculating tips in restaurants, understanding nutrition labels on food products, interpreting sale prices in shops, and determining the percentage of completion on a project.
Advanced Percentage Calculations: Finding the Whole or the Part
While calculating the percentage from the part and the whole is straightforward, there are situations where you might need to find either the part or the whole, given the percentage and either the part or the whole, respectively. Let's explore these scenarios:
1. Finding the Part, given the Whole and the Percentage:
The formula is modified as follows:
(Percentage/100) * Whole = Part
For example, if you want to find 25% of 80:
(25/100) * 80 = 20
Therefore, 25% of 80 is 20.
2. Finding the Whole, given the Part and the Percentage:
The formula is further adapted to:
(Part / (Percentage/100)) = Whole
For example, if 15 is 30% of a certain number, what is that number?
(15 / (30/100)) = 50
Therefore, 15 is 30% of 50.
Percentage Increase and Decrease: A Crucial Aspect
Percentage changes are crucial in many situations, especially when analyzing trends and growth rates.
1. Percentage Increase:
This measures the relative increase in a quantity. The formula is:
((New Value - Old Value) / Old Value) * 100 = Percentage Increase
For example, if a stock price increases from $50 to $60, the percentage increase is:
((60 - 50) / 50) * 100 = 20%
2. Percentage Decrease:
This measures the relative decrease in a quantity. The formula is:
((Old Value - New Value) / Old Value) * 100 = Percentage Decrease
For example, if a product's price decreases from $100 to $80, the percentage decrease is:
((100 - 80) / 100) * 100 = 20%
Beyond the Basics: Compound Interest and More
The concepts discussed above provide a solid foundation for understanding and applying percentages. However, there are more advanced concepts that build upon these fundamentals. One significant example is compound interest.
Compound interest is the interest earned on both the principal amount and the accumulated interest from previous periods. It's a powerful concept that dramatically affects investments and loans over time. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is critical for making informed financial decisions.
Conclusion: Mastering Percentages for Success
The seemingly simple question of "3 is what percentage of 18?" has led us on a journey into the world of percentages, revealing their importance and versatility. From basic calculations to advanced concepts like compound interest, a thorough understanding of percentages is invaluable in various fields. By mastering these techniques, you'll be better equipped to analyze data, make informed decisions, and navigate the numerical landscape of everyday life and professional endeavors. Remember the fundamental formula, practice applying it in different scenarios, and continue exploring the rich mathematical world of percentages.
Latest Posts
Latest Posts
-
120 Centimeters Equals How Many Inches
Apr 28, 2025
-
Write The Chemical Equation For Cellular Respiration
Apr 28, 2025
-
What Is 40 Degrees C In F
Apr 28, 2025
-
2 Is What Percent Of 100
Apr 28, 2025
-
What Percentage Is 39 Out Of 50
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percentage Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.