3 Of 15 Is What Percent
Kalali
Apr 16, 2025 · 5 min read
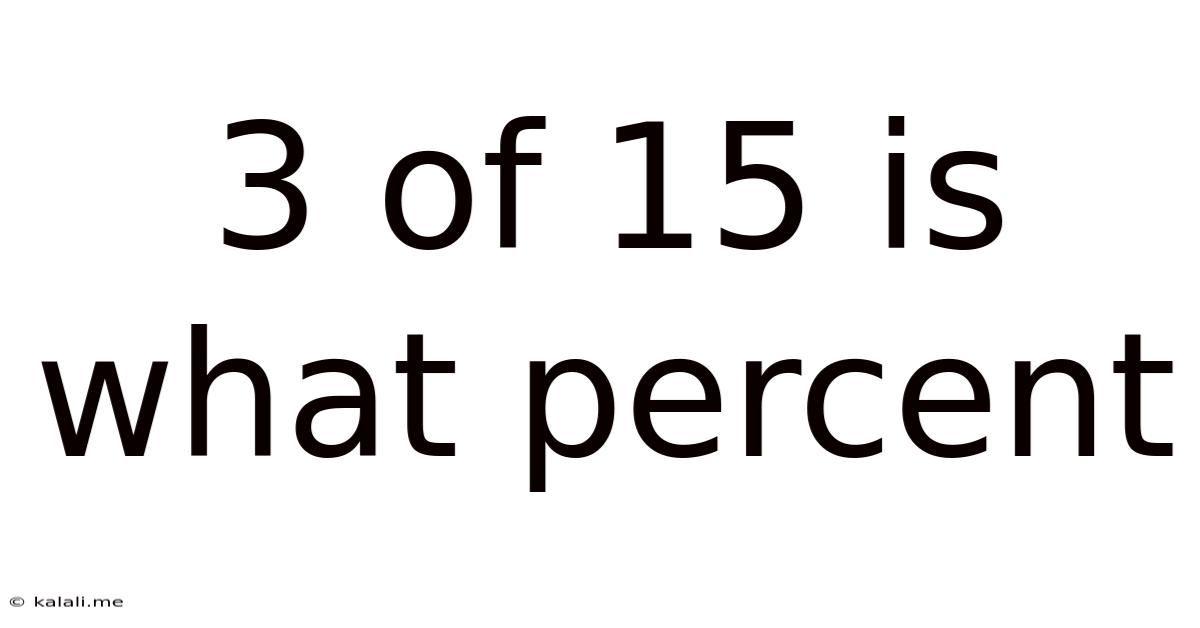
Table of Contents
3 out of 15 is What Percent? Understanding Percentages and Their Applications
Finding percentages is a fundamental skill with broad applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial reports. This article will thoroughly explore how to determine what percentage 3 out of 15 represents, providing a step-by-step guide and expanding on the broader concept of percentage calculations. We’ll cover different methods, practical examples, and even delve into advanced applications. Understanding this seemingly simple calculation opens doors to a deeper comprehension of proportional relationships and their significance in various fields.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. It represents a proportion or ratio out of a whole. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are crucial for comparing proportions, analyzing data, and making informed decisions across diverse domains.
Method 1: Using the Basic Percentage Formula
The most straightforward method to determine what percentage 3 out of 15 represents is using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 3 (the number we're interested in)
- Whole: 15 (the total number)
Let's plug these values into the formula:
(3 / 15) x 100% = 0.2 x 100% = 20%
Therefore, 3 out of 15 is 20%.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 3/15. Both the numerator (3) and the denominator (15) are divisible by 3:
3 / 15 = 1 / 5
Now, converting the simplified fraction 1/5 to a percentage:
(1 / 5) x 100% = 0.2 x 100% = 20%
This method demonstrates that simplifying the fraction first can sometimes make the calculation easier. This is particularly helpful when dealing with larger numbers.
Method 3: Using Proportions
We can also solve this problem using proportions. We can set up a proportion where x represents the percentage we're trying to find:
3/15 = x/100
To solve for x, we can cross-multiply:
15x = 300
Divide both sides by 15:
x = 20
Therefore, 3 out of 15 is 20%. This method highlights the relationship between fractions and percentages as equivalent representations of proportions.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends beyond simple arithmetic. Here are some real-world examples where this skill proves invaluable:
- Sales and Discounts: If a store offers a 20% discount on an item, knowing how to calculate percentages helps you determine the actual price reduction.
- Tax Calculations: Calculating sales tax or VAT involves determining a percentage of the total purchase price.
- Grade Calculation: Many grading systems use percentages to represent a student's performance on tests and assignments.
- Financial Analysis: Investors frequently analyze financial statements, using percentages to understand profitability, growth rates, and other key performance indicators (KPIs).
- Data Analysis and Statistics: Percentages are fundamental in representing data in charts, graphs, and statistical analyses. They allow for easy comparison and interpretation of trends.
- Survey Results: Surveys often present results in percentages, making it easier to understand the distribution of opinions or responses.
- Probability and Risk Assessment: Percentages are used to express probabilities and chances of certain events occurring.
- Cooking and Baking: Recipes often use percentages when describing ingredient ratios, especially in more advanced baking. For example, the percentage of hydration in bread baking refers to the ratio of water to flour.
Advanced Percentage Calculations
While calculating 3 out of 15 is a straightforward example, percentage calculations can become more complex. Here are some advanced scenarios:
- Percentage Increase/Decrease: Calculating the percentage increase or decrease between two values involves finding the difference between the values, dividing by the original value, and multiplying by 100%.
- Percentage Change Over Time: Tracking percentage changes over time, such as population growth or stock prices, requires calculating the percentage change between successive periods.
- Compounding Percentages: Compound interest calculations involve applying a percentage repeatedly over time. This is crucial for understanding investment returns and loan repayments.
- Weighted Averages: Weighted averages involve assigning different weights to different values based on their relative importance. This is common in academic grading and financial analysis.
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Try solving various problems with different numbers and contexts.
- Understand the Concepts: Focus on grasping the underlying concepts of fractions, ratios, and proportions.
- Use Different Methods: Experiment with different methods (formula, simplifying fractions, proportions) to find the approach that works best for you.
- Utilize Calculators and Software: For more complex calculations, utilize calculators or spreadsheet software to save time and ensure accuracy.
- Check Your Work: Always double-check your calculations to avoid errors.
Conclusion: The Significance of Understanding Percentages
The seemingly simple question "3 out of 15 is what percent?" opens the door to a vast world of applications. Understanding percentage calculations is crucial for navigating everyday life and tackling more complex mathematical and analytical tasks. From everyday shopping to complex financial decisions, the ability to accurately calculate and interpret percentages empowers individuals to make informed choices and understand the world around them more effectively. Mastering this skill provides a solid foundation for further exploration of mathematical concepts and their diverse applications in various fields. By combining the basic understanding of the formula with practice and exposure to different scenarios, one can become proficient in performing and interpreting percentage calculations with confidence. This fundamental skill is essential for success in many areas of life, both personal and professional.
Latest Posts
Latest Posts
-
What Is 0 06 As A Fraction
Apr 19, 2025
-
How Much Is 2 5 Fluid Ounces
Apr 19, 2025
-
What Era Do We Live In
Apr 19, 2025
-
How Much Feet Is 45 Inches
Apr 19, 2025
-
What Is 1 8 Of 100
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 3 Of 15 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.