3 Times 3 Times 3 Times 3 Times 3
Kalali
Jul 28, 2025 · 5 min read
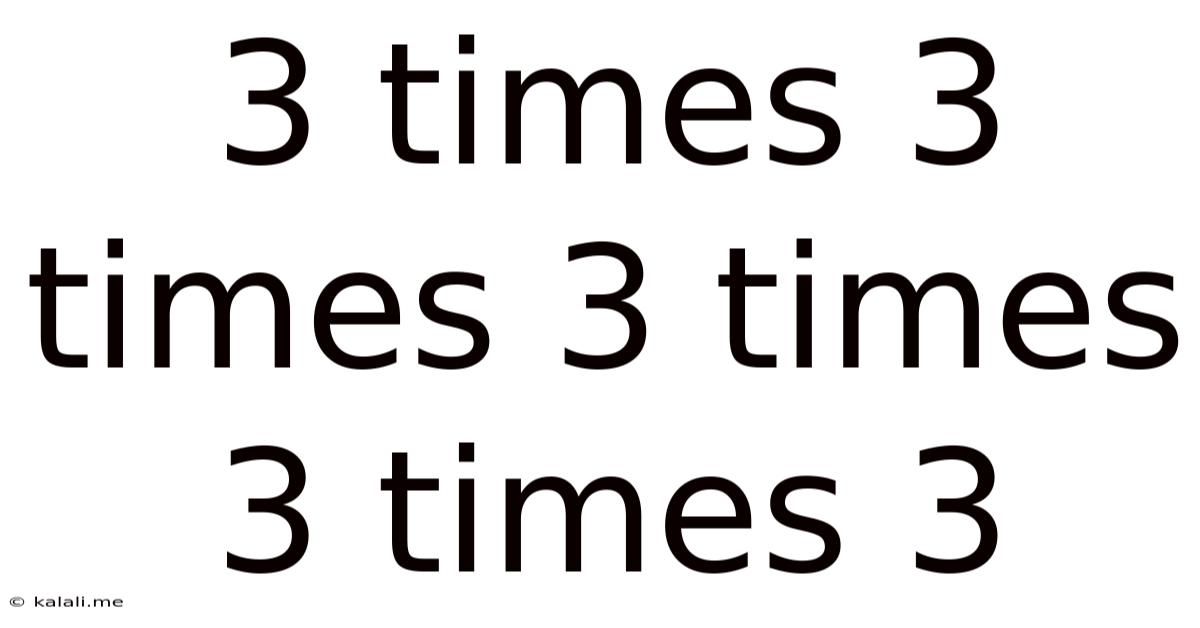
Table of Contents
Exploring the Mathematical and Philosophical Implications of 3⁵: 3 Times 3 Times 3 Times 3 Times 3
This article delves into the seemingly simple mathematical expression 3⁵ (3 times 3 times 3 times 3 times 3), revealing its multifaceted nature and exploring its implications beyond basic arithmetic. We'll unpack its mathematical significance, examine its presence in various fields, and even touch upon its potential symbolic interpretations. Understanding this seemingly simple equation opens doors to a deeper appreciation of mathematics, its applications, and its subtle philosophical underpinnings.
What is 3⁵? The Fundamentals
At its core, 3⁵ is an exponent calculation. It represents the repeated multiplication of the base number, 3, by itself five times. This results in 3 x 3 x 3 x 3 x 3 = 243. This basic calculation forms the foundation upon which we can build a richer understanding. It's a seemingly small number, but its implications are far-reaching. This seemingly simple calculation is a cornerstone of numerous mathematical concepts and applications.
3⁵ in the Realm of Mathematics
The calculation of 3⁵ demonstrates fundamental concepts in algebra and arithmetic. It showcases the power of exponential notation, a concise way to represent repeated multiplication. Understanding exponents is crucial for various mathematical operations, including:
-
Polynomial Equations: Exponents are integral to understanding and solving polynomial equations, which are fundamental in areas like calculus and physics. The concept of a third-degree polynomial, for example, directly relates to the exponent 3.
-
Geometric Sequences: Exponential growth, as exemplified by 3⁵, is a key characteristic of geometric sequences. These sequences have applications in various fields like finance (compound interest), biology (population growth), and computer science (algorithmic complexity).
-
Logarithms: The inverse operation of exponentiation is the logarithm. Understanding logarithms, often used to simplify complex calculations involving exponents, is crucial in many scientific and engineering disciplines. Solving for x in the equation 3ˣ = 243 requires the use of logarithms.
-
Modular Arithmetic: In modular arithmetic, remainders after division are the focus. The result of 3⁵ (243) can be analyzed within a specific modulus, revealing properties that might not be immediately obvious. For example, 243 mod 5 = 3.
Applications of 3⁵ and Exponentiation in Various Fields
The concept of repeated multiplication, exemplified by 3⁵, transcends theoretical mathematics and finds practical applications in diverse fields:
-
Computer Science: Binary code, the foundation of computer operation, uses powers of 2. However, other bases, including base 3, have been explored, though less commonly used. Understanding exponentiation is crucial for algorithms and data structures.
-
Physics: Exponential functions describe various physical phenomena, such as radioactive decay, where the rate of decay is proportional to the amount of the substance remaining.
-
Finance: Compound interest, a crucial concept in finance, relies on exponential growth. Understanding exponential functions is essential for calculating future values of investments or loans.
-
Biology: Population growth, especially in ideal conditions, often follows an exponential pattern. Understanding exponentiation allows for modeling and predicting population dynamics.
Beyond the Numbers: Exploring the Symbolic and Philosophical Aspects
While 243 is the mathematical outcome of 3⁵, delving into the symbolic representation can open intriguing avenues of thought. The number 3 itself holds significant symbolic weight across numerous cultures and belief systems:
-
Religious Significance: The number 3 frequently appears in religious contexts, often symbolizing the trinity (father, son, and holy spirit in Christianity, for example). The repeated multiplication could be seen as emphasizing this threefold nature, amplifying its significance.
-
Philosophical Interpretations: The repeated multiplication might be interpreted as representing iterative processes or cycles of growth and change. Each multiplication of 3 could represent a stage in a process, culminating in the final result of 243.
-
Geometric Representations: Imagine a cube, a three-dimensional shape. The volume of the cube is calculated using the formula side x side x side (s³). Extending this concept to higher dimensions (hypercubes), we can visualize further multiplications, providing a spatial interpretation of exponential growth.
3⁵ in the Context of Other Mathematical Concepts
-
Prime Factorization: The number 243 (3⁵) has a simple prime factorization: 3 x 3 x 3 x 3 x 3. This highlights its relationship to prime numbers and the fundamental building blocks of numbers.
-
Perfect Numbers: Although 243 is not a perfect number (a number equal to the sum of its proper divisors), exploring its relationship to other number theory concepts can uncover further mathematical connections.
-
Fibonacci Sequence: While not directly related to the Fibonacci sequence, comparing the growth rate of 3⁵ to the exponential growth of the Fibonacci sequence in the long run provides an interesting comparison of different mathematical growth patterns.
-
Pascal's Triangle: While not explicitly showing 243, examining Pascal's Triangle and its relationship to binomial expansions can provide insights into combinatorial mathematics, a field where exponents often play a crucial role.
Advanced Applications and Further Exploration
-
Fractals: Fractals, complex geometric shapes with self-similar patterns, often involve iterative processes and exponential relationships, providing visual representations of exponential growth. Analyzing the relationship between 3⁵ and fractal geometry can lead to deeper insights.
-
Game Theory: In game theory, exponential functions can model strategic interactions and the growth of payoffs in repeated games. Understanding exponential growth is crucial for analyzing these complex scenarios.
Conclusion: The Enduring Significance of 3⁵
The seemingly simple calculation of 3⁵, while resulting in the straightforward answer of 243, unveils a surprisingly rich tapestry of mathematical, scientific, and philosophical implications. From its foundational role in algebra to its applications in diverse fields and even its potential symbolic interpretations, this equation demonstrates the interconnectedness of various concepts. By exploring 3⁵, we gain a deeper appreciation not only for mathematical principles but also for the power of seemingly simple equations to reveal profound complexities within our world. The journey beyond the calculation itself provides a valuable lesson in the depth and breadth of mathematical exploration, highlighting the endless possibilities for discovery within seemingly simple concepts. Further exploration into the mathematical ideas presented here will undoubtedly reveal even more fascinating connections and applications. The seemingly simple equation, 3⁵, truly serves as a gateway to a wider mathematical universe.
Latest Posts
Latest Posts
-
How Fast Is 300 Kilometers In Miles Per Hour
Jul 28, 2025
-
A 31 Foot Board Is Cut Into Two Pieces
Jul 28, 2025
-
720 080 In Expanded Form With Exponents
Jul 28, 2025
-
How Many Potato Chips In An Ounce
Jul 28, 2025
-
How Many Mini Marshmallows Equal One Large Marshmallow
Jul 28, 2025
Related Post
Thank you for visiting our website which covers about 3 Times 3 Times 3 Times 3 Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.