3 X 3 X 3 X 3 X 3
Kalali
Jul 26, 2025 · 6 min read
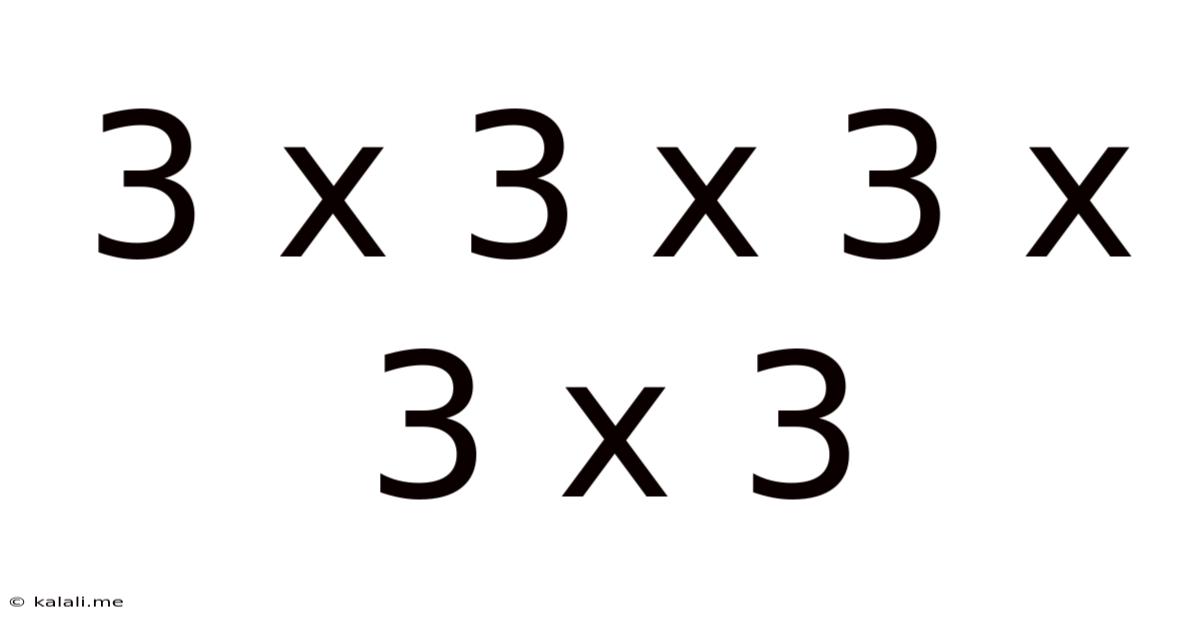
Table of Contents
Exploring the Mathematical Landscape of 3 x 3 x 3 x 3 x 3: Beyond Simple Multiplication
This article delves into the seemingly simple mathematical expression, 3 x 3 x 3 x 3 x 3, exploring its various facets and implications across different mathematical fields. While the calculation itself is straightforward, its underlying principles and extensions offer a rich tapestry of mathematical concepts, from basic arithmetic to more advanced topics like exponential notation and its applications in real-world scenarios. We'll unpack this seemingly simple equation, revealing its surprising depth and breadth.
Meta Description: This in-depth article explores the mathematical expression 3 x 3 x 3 x 3 x 3, going beyond simple calculation to uncover its significance in various mathematical contexts, from exponents and powers to real-world applications. Discover the fascinating world of numbers hidden within this seemingly basic equation.
Understanding the Fundamentals: Repeated Multiplication
At its core, 3 x 3 x 3 x 3 x 3 represents repeated multiplication. This is a fundamental arithmetic operation where a number is multiplied by itself a certain number of times. In this specific case, the number 3 is multiplied by itself five times. This repetitive process is the foundation for understanding exponents and powers, which we will explore further. The result of this calculation, 243, is the fifth power of 3.
Exponential Notation: A More Concise Representation
The repeated multiplication of 3 x 3 x 3 x 3 x 3 can be expressed more concisely using exponential notation. Exponential notation uses a base number (in this case, 3) and an exponent (in this case, 5) to represent repeated multiplication. The expression is written as 3⁵, where 3 is the base and 5 is the exponent. The exponent indicates how many times the base is multiplied by itself. This notation is significantly more efficient for representing very large repeated multiplications.
Calculating 3⁵: Different Approaches
While a simple calculator readily provides the answer (243), understanding the process of calculating 3⁵ is crucial. We can approach this in several ways:
-
Sequential Multiplication: The most straightforward method is to perform the multiplication sequentially: 3 x 3 = 9; 9 x 3 = 27; 27 x 3 = 81; 81 x 3 = 243. This approach clearly demonstrates the repeated multiplication process.
-
Grouping: We can group the multiplications to simplify the calculation. For example: (3 x 3) x (3 x 3) x 3 = 9 x 9 x 3 = 81 x 3 = 243. This method highlights the potential for strategic simplification in more complex calculations.
-
Using a Calculator or Computer: For larger exponents or more complex calculations, using a calculator or computer program is the most efficient approach.
The Significance of Exponents in Mathematics
Exponents are a cornerstone of many mathematical concepts and applications. Their significance stems from their ability to represent and manipulate very large or very small numbers efficiently. Understanding exponents is crucial for:
-
Scientific Notation: Used to express extremely large or small numbers, such as those encountered in physics, astronomy, and chemistry. For example, the speed of light can be expressed in scientific notation using exponents.
-
Polynomial Equations: Exponents are fundamental in polynomial equations, which are used to model various phenomena in many fields, including engineering, finance, and computer science.
-
Calculus: Exponents play a critical role in calculus, specifically in differentiation and integration. Understanding exponents is essential for mastering concepts like derivatives and integrals.
-
Compound Interest: In finance, understanding exponents is crucial for calculating compound interest, where interest is earned not only on the principal but also on accumulated interest. The formula for compound interest involves exponents.
Exploring Related Mathematical Concepts
The expression 3 x 3 x 3 x 3 x 3 and its exponential representation, 3⁵, opens the door to exploring various related mathematical concepts:
-
Logarithms: Logarithms are the inverse of exponents. If 3⁵ = 243, then the logarithm base 3 of 243 is 5 (log₃243 = 5). Logarithms are used extensively in various fields, including chemistry, physics, and computer science.
-
Powers and Roots: The expression 3⁵ involves a power (the fifth power of 3). Conversely, finding the fifth root of 243 (⁵√243) would give us 3. Understanding powers and roots is essential for solving various mathematical equations.
-
Sequences and Series: The numbers generated by raising 3 to successive powers (3¹, 3², 3³, 3⁴, 3⁵, etc.) form a geometric sequence. Understanding sequences and series is crucial for various mathematical applications.
Real-World Applications: Where 3⁵ and Similar Calculations Matter
While seemingly abstract, the concepts illustrated by 3 x 3 x 3 x 3 x 3 have tangible real-world applications:
-
Growth and Decay: Exponential functions, such as 3⁵, are used to model growth and decay processes in various fields. For example, population growth, radioactive decay, and compound interest can all be modeled using exponential functions.
-
Computer Science: Exponential growth and decay are fundamental concepts in computer science, particularly in algorithm analysis and data structures. The efficiency of algorithms is often expressed using Big O notation, which involves exponents.
-
Physics and Engineering: Exponential functions are crucial in physics and engineering for modeling phenomena such as radioactive decay, capacitor discharge, and signal attenuation.
Expanding the Exploration: Variations and Extensions
We can extend our exploration of 3 x 3 x 3 x 3 x 3 by considering:
-
Different Bases: We can explore similar calculations with different bases, such as 2⁵, 4⁵, or even fractional bases. This broadens our understanding of exponential functions and their behavior.
-
Larger Exponents: We can examine the results of raising 3 to larger exponents (3¹⁰, 3²⁰, etc.) to appreciate the rapid growth of exponential functions.
-
Negative Exponents: Exploring negative exponents (3⁻⁵) introduces the concept of reciprocals and further expands our understanding of exponential functions.
-
Fractional Exponents: Examining fractional exponents (e.g., 3^(1/2), which is the square root of 3) introduces the concept of roots and extends the applicability of exponential notation.
Conclusion: The Unfolding Richness of a Simple Equation
The seemingly simple equation, 3 x 3 x 3 x 3 x 3, serves as a gateway to a vast and intricate world of mathematical concepts and applications. From basic arithmetic to advanced calculus and real-world modeling, the principles embedded within this equation are fundamental to numerous fields. By exploring its various facets, we gain a deeper appreciation for the power and elegance of mathematics and its profound influence on our understanding of the world around us. This seemingly simple calculation highlights the interconnectedness of mathematical concepts and underscores the importance of building a strong foundational understanding of fundamental arithmetic principles. The journey from simple multiplication to understanding exponential growth and its far-reaching implications showcases the beauty and utility of mathematics in its entirety.
Latest Posts
Latest Posts
-
What Is A Legend In A Graph
Jul 26, 2025
-
How Long Does Chicken Broth Last Unopened
Jul 26, 2025
-
How Many Sq In A Box Of Siding
Jul 26, 2025
-
What Is A Half Of One Third
Jul 26, 2025
-
How Many Months Have 5 Weeks In Them
Jul 26, 2025
Related Post
Thank you for visiting our website which covers about 3 X 3 X 3 X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.