30 Increased By 3 Times The Square Of A Number
Kalali
Aug 07, 2025 · 6 min read
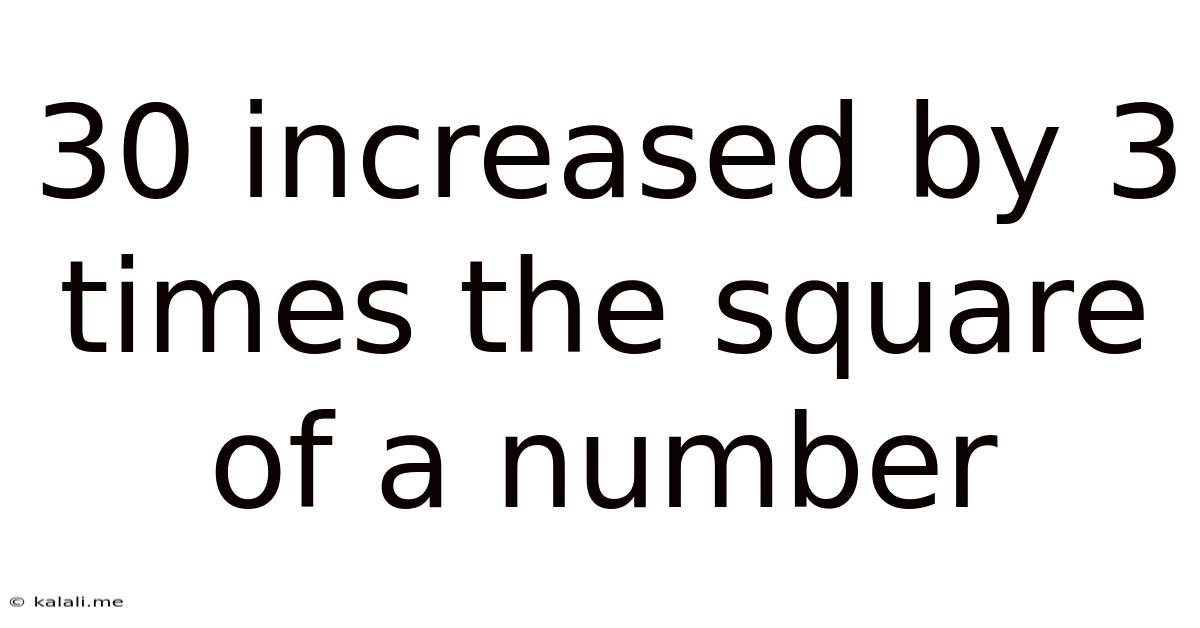
Table of Contents
Exploring the Mathematical Landscape of "30 Increased by 3 Times the Square of a Number"
This seemingly simple phrase, "30 increased by 3 times the square of a number," opens a door to a fascinating exploration of algebra, equation solving, and the various ways we can represent and interpret mathematical relationships. This article delves deep into the problem, examining its different interpretations, solutions, and the broader mathematical concepts it illuminates. We'll cover solving the equation, exploring graphical representations, analyzing potential real-world applications, and even touching upon the historical context of such problems. Understanding this seemingly simple phrase unlocks a wealth of mathematical understanding.
Understanding the Problem: From Words to Equations
The phrase "30 increased by 3 times the square of a number" can be translated into a mathematical equation. Let's represent the "number" with the variable x. The phrase then translates to:
30 + 3x²
This expression represents the result of adding 30 to three times the square of a number (x). However, the problem usually isn't just about forming an expression; it's typically framed as an equation, often requiring us to find the value(s) of x that satisfy a specific condition. For instance, the complete problem might be:
"Find the number(s) such that 30 increased by 3 times the square of the number equals a given value (y)."
This leads us to the equation:
30 + 3x² = y
Where 'y' represents the given value. The challenge then becomes solving this quadratic equation for x.
Solving the Quadratic Equation: Different Approaches
The equation 30 + 3x² = y is a quadratic equation, meaning it involves the square of the unknown variable (x). Solving quadratic equations involves several methods, each with its own advantages and disadvantages. Let's explore some common approaches:
1. Rearranging the Equation:
The first step is to rearrange the equation into standard quadratic form: ax² + bx + c = 0. In our case, we subtract 'y' from both sides:
3x² - y + 30 = 0
Now we have a = 3, b = 0, and c = 30 - y.
2. Using the Quadratic Formula:
The quadratic formula is a powerful tool for solving any quadratic equation. It states:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values, we get:
x = [± √( -4 * 3 * (30 - y))] / (2 * 3)
x = [± √(-12(30 - y))] / 6
x = ± √(-12(30 - y)) / 6
This formula reveals a crucial aspect: the value of 'y' significantly impacts the solution. The expression under the square root, -12(30 - y), must be non-negative for real solutions to exist. This means:
-12(30 - y) ≥ 0
Solving this inequality, we find:
y ≥ 30
This implies that only values of 'y' greater than or equal to 30 will yield real solutions for x. If y < 30, the solutions for x will be complex numbers (involving the imaginary unit 'i').
3. Factoring (When Possible):
Factoring is a simpler method if the quadratic equation can be easily factored. However, this is not always possible. Let's consider a specific example:
Let's say y = 60. Our equation becomes:
3x² - 60 + 30 = 0
3x² - 30 = 0
3x² = 30
x² = 10
x = ±√10
In this case, factoring was straightforward, leading to two real solutions: x = √10 and x = -√10.
4. Completing the Square:
Completing the square is another method to solve quadratic equations, especially useful when the quadratic formula is cumbersome or when dealing with equations that don't factor easily. This method involves manipulating the equation to create a perfect square trinomial. However, for our equation, the quadratic formula or factoring (if possible) are usually more efficient.
Graphical Representation and Interpretation
The equation 30 + 3x² = y can be graphically represented by plotting the function y = 3x² + 30. This is a parabola that opens upwards (since the coefficient of x² is positive). The vertex of the parabola is at (0, 30), representing the minimum value of 'y'. The graph visually demonstrates that as x increases (either positively or negatively), the value of 'y' also increases. The graph also illustrates the solutions for a given 'y': the x-coordinates of the points where the horizontal line y = (given value) intersects the parabola. If the line doesn't intersect the parabola, there are no real solutions, confirming our earlier finding that y must be ≥ 30 for real solutions.
Real-World Applications
While this might seem like a purely abstract mathematical exercise, equations like this find applications in various fields:
-
Physics: In projectile motion, the height of an object at a given time can be modeled using a quadratic equation. The initial height (30) can be analogous to the initial height of the projectile, and the term 3x² could represent the effect of gravity on its vertical displacement.
-
Engineering: Calculating the area or volume of certain shapes involves quadratic equations. For example, determining the dimensions of a container to hold a specific volume might lead to an equation of this form.
-
Economics: Quadratic equations can model certain economic relationships, such as cost functions, where x might represent the quantity produced, and y represents the total cost. The constant term (30) might represent fixed costs, and the quadratic term could represent variable costs.
-
Computer Science: Solving quadratic equations is essential in algorithms for optimization and in computer graphics.
Expanding the Problem: Variations and Extensions
The core problem can be extended in several ways, increasing its complexity and revealing further mathematical insights:
-
Inequalities: Instead of asking for the value of x where 30 + 3x² equals a specific value, we could ask for the range of x where 30 + 3x² is greater than or less than a given value. This leads to solving quadratic inequalities.
-
Systems of Equations: We could introduce another equation involving x and create a system of equations that needs to be solved simultaneously.
-
Higher-Order Polynomials: Instead of a quadratic equation, we could explore similar problems involving cubic or higher-order polynomials.
Historical Context and Mathematical Significance
Solving quadratic equations has a rich history, dating back to ancient Babylonian and Egyptian civilizations. The development of methods for solving these equations was a significant milestone in the history of mathematics, paving the way for more advanced algebraic techniques. The understanding of quadratic equations forms a fundamental building block for more advanced mathematical concepts encountered in calculus, linear algebra, and beyond.
Conclusion
The seemingly simple problem of "30 increased by 3 times the square of a number" is far richer than it initially appears. By analyzing this problem, we've explored various methods for solving quadratic equations, considered its graphical representation, explored potential real-world applications, and touched upon its historical significance. This exploration highlights the interconnectedness of different mathematical concepts and underscores the importance of problem-solving skills in mathematics. It showcases how a single mathematical expression can be a gateway to a vast and fascinating mathematical landscape.
Latest Posts
Latest Posts
-
Five Letter Word Second Letter I Fifth Letter E
Aug 10, 2025
-
How Much Is 96 Oz Of Water
Aug 10, 2025
-
How Long Would It Take To Drive 12 Miles
Aug 10, 2025
-
How Many 8ths Are In An Inch
Aug 10, 2025
-
How Long Does It Take To Drive 1800 Miles
Aug 10, 2025
Related Post
Thank you for visiting our website which covers about 30 Increased By 3 Times The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.