30 Is What Percent Of 40
Kalali
Mar 29, 2025 · 5 min read
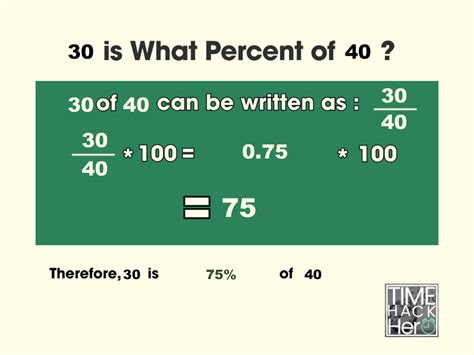
Table of Contents
30 is What Percent of 40: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous areas of life, from everyday budgeting and shopping to more complex fields like finance and statistics. Understanding how to solve percentage problems is crucial for making informed decisions and interpreting data accurately. This article will delve deep into the question, "30 is what percent of 40?", providing a step-by-step solution, exploring different approaches, and expanding on the broader concept of percentage calculations.
Understanding Percentages
Before diving into the specific problem, let's establish a firm grasp on what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," literally meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Solving "30 is What Percent of 40?"
The question, "30 is what percent of 40?", can be expressed mathematically as:
30 = x% of 40
where 'x' represents the unknown percentage we need to find. There are several ways to solve this equation.
Method 1: Using the Percentage Formula
The most common method involves using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 30 (the value we're comparing)
- Whole: 40 (the total value)
Substituting these values into the formula, we get:
(30 / 40) x 100 = x%
(0.75) x 100 = x%
x = 75%
Therefore, 30 is 75% of 40.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
30/40 = x/100
To solve for 'x', we cross-multiply:
30 x 100 = 40 x x
3000 = 40x
x = 3000 / 40
x = 75
Therefore, x = 75%, confirming our previous result.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
1. Calculating Discounts and Sales Tax
Retail stores frequently advertise discounts as percentages. If a $100 item is on sale for 20% off, you can calculate the discount and the final price using percentage calculations.
- Discount: 20% of $100 = (20/100) x $100 = $20
- Final Price: $100 - $20 = $80
Sales tax is another common application. If the sales tax rate is 6%, you can calculate the tax amount and the total cost of a purchase.
2. Analyzing Financial Statements
In finance, percentages are essential for analyzing financial statements like income statements and balance sheets. Profit margins, return on investment (ROI), and debt-to-equity ratios are all expressed as percentages. These metrics provide crucial insights into a company's financial health and performance.
3. Understanding Statistical Data
Percentages are frequently used to present and interpret statistical data. For example, survey results, election polls, and market research reports often express findings as percentages to make the data more easily understandable and comparable.
4. Calculating Grades and Performance Metrics
In education, percentages are used to calculate grades and assess student performance. A score of 85 out of 100 translates to an 85% grade. Similar percentage-based metrics are utilized to evaluate employee performance in various workplaces.
5. Determining Growth Rates
Percentages are crucial for measuring growth rates in various contexts. For instance, population growth, economic growth, and investment returns are often expressed as percentage increases or decreases over time.
Beyond the Basics: More Complex Percentage Problems
While "30 is what percent of 40?" is a relatively straightforward problem, the concept of percentages extends to more complex calculations. These might include:
- Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a stock price rises from $50 to $60, the percentage increase can be calculated as [(60-50)/50] x 100 = 20%.
- Finding the Original Value: Determining the original value after a percentage change has occurred. If a price increased by 10% to reach $110, the original price was $100 ($110 / 1.10 = $100).
- Compound Interest: Calculating interest earned on both the principal and accumulated interest over time. This involves repeated percentage calculations.
- Percentage Points: Understanding the difference between percentage change and percentage points. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve a variety of problems to build your understanding and confidence.
- Use a Calculator: Don't hesitate to use a calculator, especially for more complex calculations. This will save you time and reduce the risk of errors.
- Visual Aids: Diagrams and charts can be helpful in visualizing percentage problems, especially when dealing with complex scenarios.
- Break Down Complex Problems: If faced with a challenging problem, break it down into smaller, more manageable steps.
Conclusion: The Power of Percentage Understanding
Understanding percentages is a fundamental skill with widespread applications. From everyday finances to complex data analysis, the ability to calculate and interpret percentages effectively is crucial for making informed decisions and navigating the world around us. The simple problem of "30 is what percent of 40?" serves as a springboard to understanding the broader concept of percentages and their significance in various aspects of life. By mastering this fundamental skill and exploring its diverse applications, you'll significantly enhance your problem-solving capabilities and decision-making processes. Remember consistent practice is key to mastery, so keep practicing and expanding your knowledge in this crucial area.
Latest Posts
Latest Posts
-
22 Degrees Celsius Is What Fahrenheit
Mar 31, 2025
-
How Many Cups Are In 80 Ounces
Mar 31, 2025
-
1 1 2 Inch Convert To Mm
Mar 31, 2025
-
250 Cm Is How Many Inches
Mar 31, 2025
-
Similarities Between Inner Planets And Outer Planets
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 30 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
