30 Out Of 35 As A Percentage
Kalali
Mar 11, 2025 · 5 min read
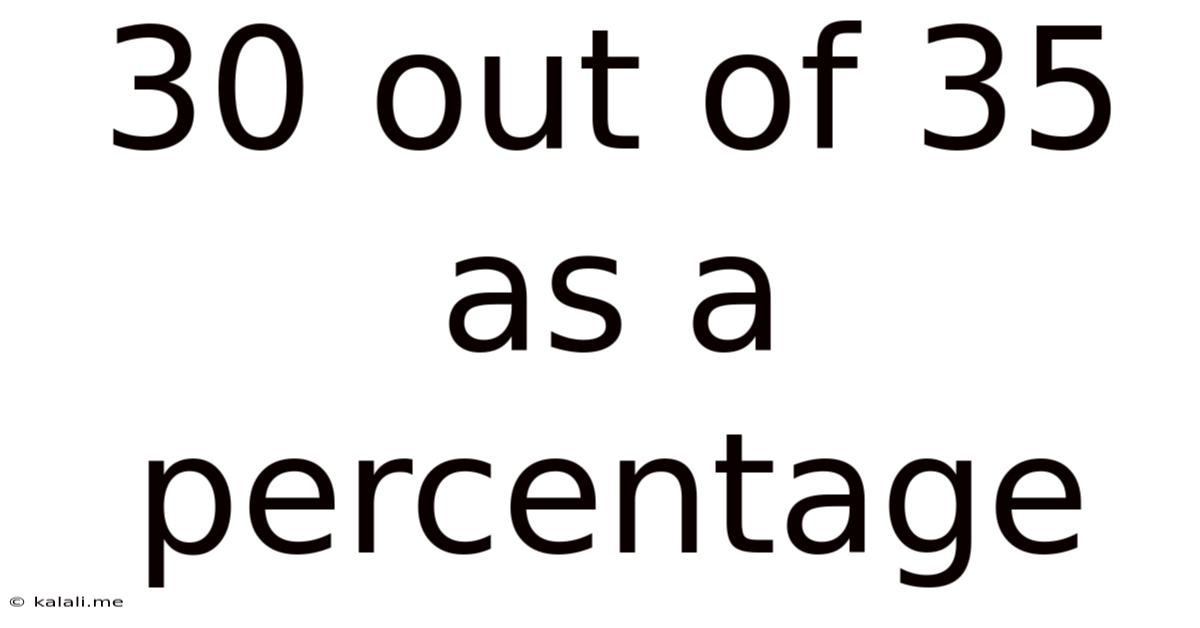
Table of Contents
30 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in various aspects of life, from academic assessments to financial transactions. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This comprehensive guide will delve into the calculation of "30 out of 35 as a percentage," exploring different methods, applications, and related concepts. We'll also discuss the broader implications of percentage calculations and their importance in everyday life.
Understanding the Basics of Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." Therefore, 50% signifies 50 out of 100, which is equivalent to the fraction ½ or 0.5 as a decimal.
Calculating 30 out of 35 as a Percentage: Method 1 (Fraction to Decimal to Percentage)
This method involves three straightforward steps:
-
Express as a Fraction: The phrase "30 out of 35" translates directly to the fraction 30/35.
-
Convert to a Decimal: Divide the numerator (30) by the denominator (35): 30 ÷ 35 = 0.857142857... We can round this to a reasonable number of decimal places, such as 0.86.
-
Convert to a Percentage: Multiply the decimal by 100: 0.86 x 100 = 86%.
Therefore, 30 out of 35 is approximately 86%. The slight rounding introduces a minor margin of error, but for most practical purposes, 86% is an accurate representation.
Calculating 30 out of 35 as a Percentage: Method 2 (Direct Proportion)
This method utilizes the concept of proportions to solve the problem directly:
We can set up a proportion:
30/35 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
35x = 3000
Then, divide both sides by 35:
x = 3000 ÷ 35 = 85.7142857...
Rounding to the nearest whole number, we again obtain 86%.
Understanding the Significance of the Result
The result, 86%, signifies that 30 represents 86% of the total value of 35. This information is valuable in various contexts. For example, if 35 represents the total number of questions on a test, and a student answered 30 correctly, their score would be 86%. Similarly, if 35 represents a total budget, and 30 has been spent, then 86% of the budget has been utilized.
Applications of Percentage Calculations in Real-Life Scenarios
Percentage calculations are ubiquitous in everyday life, encompassing a broad range of situations:
- Academic Performance: Calculating grades, assessing test scores, and determining overall academic progress.
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, applying discounts, and calculating markups.
- Statistics: Analyzing data, representing proportions, and interpreting survey results.
- Science: Expressing concentrations, measuring changes, and representing experimental data.
- Sports: Calculating batting averages, win percentages, and player statistics.
Beyond the Calculation: Working with Percentages Effectively
While knowing how to calculate percentages is essential, understanding how to use them effectively is equally important. This involves:
-
Rounding: Determining the appropriate level of precision when rounding decimals to percentages. Overly precise percentages can be misleading, while rounding too drastically can lose important information.
-
Contextual Understanding: Always consider the context of the calculation. A small percentage change can be significant in some situations, while a large percentage change might be insignificant in others.
-
Data Interpretation: Percentages are often used to represent data visually through charts and graphs. Understanding how to interpret these visual representations of data is crucial for effective communication and analysis.
-
Problem Solving: Percentage calculations form the basis for solving many real-world problems. Learning to translate word problems into mathematical expressions is a key skill.
Advanced Percentage Calculations: Finding the Whole from a Percentage
Often, you may know a percentage and a part of the whole but need to determine the total value. For example, if 30 represents 86% of a total value, how can we calculate that total value?
We can set up a proportion:
30/x = 86/100
Cross-multiplying and solving for 'x':
86x = 3000 x = 3000/86 ≈ 34.88
Therefore, if 30 represents 86%, the total value is approximately 35. This minor discrepancy arises from the rounding we performed earlier.
Percentage Increase and Decrease
Percentage calculations are also crucial for understanding changes over time or comparing different values. For instance:
-
Percentage Increase: If a quantity increases from 30 to 35, the percentage increase is calculated as: [(35-30)/30] x 100% ≈ 16.7%
-
Percentage Decrease: Conversely, if a quantity decreases from 35 to 30, the percentage decrease is calculated as: [(35-30)/35] x 100% ≈ 14.3%
Error Analysis and Precision in Percentage Calculations
Understanding the potential for error in percentage calculations is crucial. This error can stem from:
-
Rounding Errors: Rounding numbers during the calculation introduces a degree of approximation.
-
Data Inaccuracy: If the initial data used in the calculation is inaccurate, the resulting percentage will also be inaccurate.
-
Measurement Errors: In scientific or engineering contexts, measurement errors can propagate through percentage calculations, leading to significant discrepancies.
Being mindful of these potential sources of error is critical for obtaining reliable and meaningful results.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is a valuable skill applicable across numerous disciplines and everyday situations. From understanding academic grades to navigating financial transactions and analyzing data, the ability to accurately calculate and interpret percentages is essential for informed decision-making. By understanding the different methods, applications, and potential pitfalls of percentage calculations, you can improve your problem-solving abilities and enhance your understanding of the world around you. Remember to always consider the context, check for rounding errors, and strive for accuracy and clarity in your calculations.
Latest Posts
Latest Posts
-
Which Situation Is An Example Of An Internal Conflict
Jul 05, 2025
-
What Year Was I Born If Im 65
Jul 05, 2025
-
Is An Egg A Fruit Or Vegetable
Jul 05, 2025
-
How Many Cups In A Bag Of Chocolate Chips
Jul 05, 2025
-
Spyware Can Result In All Of The Following Except
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 30 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.