31 Out Of 50 As A Percentage
Kalali
Apr 12, 2025 · 5 min read
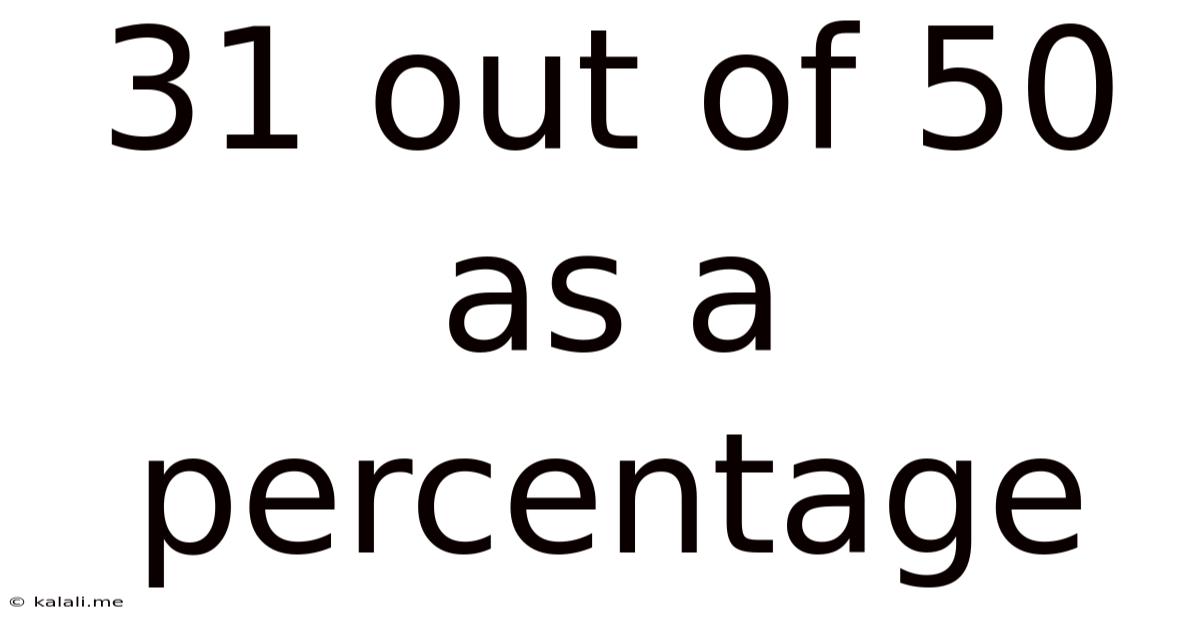
Table of Contents
31 out of 50 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and academics to everyday life. This article will delve deep into calculating percentages, focusing specifically on how to determine what percentage 31 out of 50 represents, and then expanding on various methods and applications of percentage calculations. We'll explore different approaches, including manual calculation, using calculators, and employing spreadsheet software. This comprehensive guide will equip you with the knowledge and tools to confidently tackle any percentage problem.
What percentage is 31 out of 50? The answer is 62%. But let's explore the how and why behind this answer, examining different methods and broadening our understanding of percentage calculations in the process.
Method 1: The Basic Percentage Formula
The most fundamental method for calculating percentages involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 31 (the number we're considering as a portion of the whole)
- Whole: 50 (the total number)
Plugging these values into the formula:
(31 / 50) x 100% = 0.62 x 100% = 62%
Therefore, 31 out of 50 is 62%.
Method 2: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply divide 31 by 50, and then multiply the result by 100. The calculator will directly provide the answer: 62%. This method is particularly efficient for quick calculations.
Method 3: Using Spreadsheet Software (e.g., Microsoft Excel, Google Sheets)
Spreadsheet software provides another convenient way to calculate percentages. You can input the values (31 and 50) into separate cells, and then use a formula in another cell to perform the calculation. For instance, if you enter 31 in cell A1 and 50 in cell B1, the formula =(A1/B1)*100 in cell C1 will return the percentage, 62%. This method is ideal for complex calculations involving multiple percentages or for creating dynamic worksheets where the values can be changed and the percentage automatically recalculated.
Understanding the Concept of Percentages
Percentages are a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 62% means 62 out of 100. This standardized representation allows for easy comparison and interpretation of different proportions. Understanding percentages is crucial for:
- Financial calculations: Interest rates, discounts, taxes, profit margins, and investment returns are all expressed as percentages.
- Academic assessments: Grades, test scores, and performance metrics are often presented as percentages.
- Statistical analysis: Data is frequently analyzed and presented using percentages to show proportions and trends.
- Everyday life: Tips, sales, and discounts are commonly expressed as percentages, making it essential to understand these calculations for informed decision-making.
Practical Applications of Percentage Calculations: Real-world examples
Let's consider various scenarios where understanding 31 out of 50 as 62% is helpful:
- Academic Performance: A student answered 31 out of 50 questions correctly on a test. Their score is 62%, providing a clear indication of their performance. This percentage can be compared to other students' scores or used to assess progress over time.
- Sales and Marketing: A business sold 31 out of 50 units of a product. This represents a 62% sales rate. This data is vital for inventory management, forecasting sales, and assessing marketing campaign effectiveness.
- Survey Results: In a survey of 50 people, 31 responded positively to a particular question. This indicates a 62% positive response rate. This information is crucial for understanding public opinion and informing strategic decisions.
- Quality Control: A factory inspected 50 products, finding 31 to meet quality standards. This demonstrates a 62% pass rate, informing production processes and ensuring quality control.
Beyond the Basics: More Complex Percentage Problems
While calculating 31 out of 50 is relatively straightforward, percentage calculations can become more complex. Let's explore some variations:
- Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, what is 62% of 50? The formula would be: (62/100) * 50 = 31.
- Finding the Whole: If you know the percentage and the part, you can find the whole. For example, if 31 represents 62%, what is the total? The formula would be: (31 / 0.62) = 50.
- Percentage Increase/Decrease: Calculating percentage changes involves finding the difference between two values and expressing it as a percentage of the original value. For example, an increase from 50 to 62 would be calculated as: ((62-50)/50) * 100% = 24% increase.
- Compounding Percentages: In scenarios involving multiple percentage changes, the effects are compounded. This is common in financial calculations, such as compound interest.
Avoiding Common Mistakes in Percentage Calculations
Several common mistakes can lead to inaccurate results:
- Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS). Division should be performed before multiplication.
- Confusing percentages with decimals: Ensure you convert percentages to decimals (by dividing by 100) or vice versa correctly when using them in calculations.
- Rounding errors: Be mindful of rounding errors, especially in complex calculations involving multiple percentages. Round to a suitable number of decimal places at the end of the calculation to maintain accuracy.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with widespread applications. Understanding the basic formula, utilizing calculators or spreadsheet software, and being aware of common pitfalls will enable you to confidently solve a wide range of percentage problems. From everyday transactions to complex financial analyses, the ability to work with percentages is indispensable for informed decision-making and accurate problem-solving. The example of calculating 31 out of 50 as 62% serves as a solid foundation for tackling more complex percentage calculations and real-world applications. Remember to always double-check your work and choose the method that best suits your needs and the complexity of the problem at hand.
Latest Posts
Latest Posts
-
How Long Can A Cat Hold Its Breath
Apr 13, 2025
-
What Is 10 To The Power Of 100
Apr 13, 2025
-
What Are The Two Oxidation States Of Nitrogen In Nh4no2
Apr 13, 2025
-
154 Cm To Inches And Feet
Apr 13, 2025
-
How Many Inches Is 23 5 Cm
Apr 13, 2025
Related Post
Thank you for visiting our website which covers about 31 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.