33 8 As A Mixed Number
Kalali
Apr 25, 2025 · 5 min read
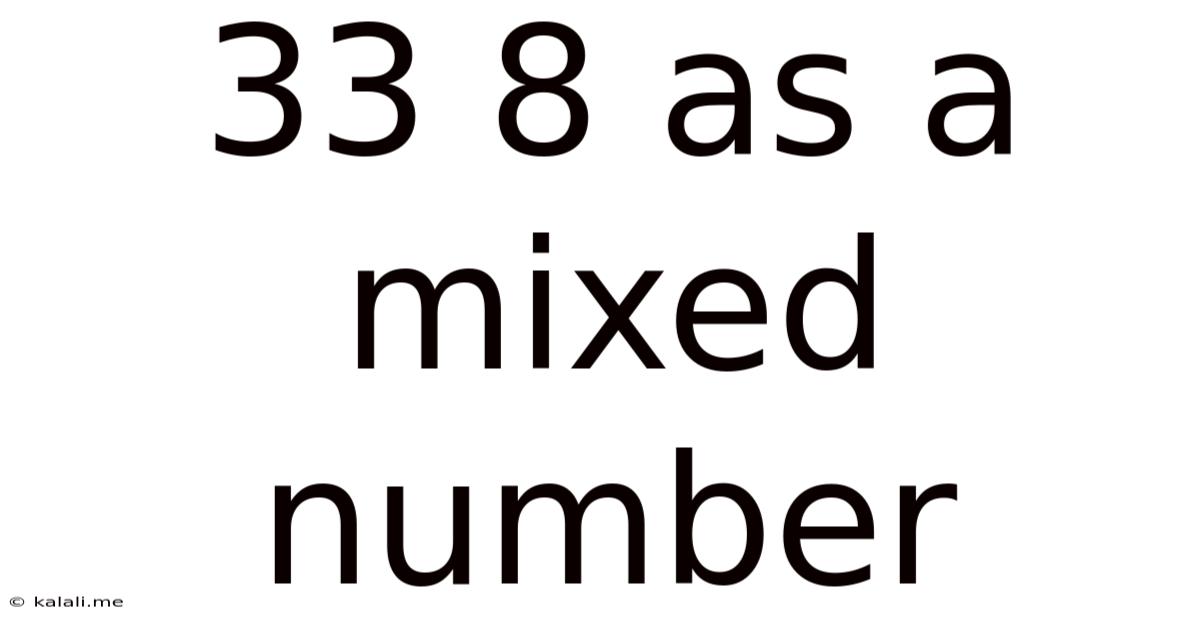
Table of Contents
Understanding 33/8 as a Mixed Number: A Comprehensive Guide
The fraction 33/8 represents a quantity larger than one whole. Understanding how to convert improper fractions, like 33/8, into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 33/8 into a mixed number but will also delve into the underlying concepts, provide multiple methods for solving similar problems, and offer practice examples to solidify your understanding. This article will also explore the practical applications of understanding mixed numbers and improper fractions, showing you why this knowledge is crucial beyond the classroom.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ½, 3 ¼, and 2 ⁷/₈ are all mixed numbers. They represent quantities greater than one.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 5/4, 11/3, and, of course, 33/8. These fractions represent quantities greater than or equal to one.
Converting 33/8 to a Mixed Number: The Standard Method
The most common method for converting an improper fraction to a mixed number involves division. We divide the numerator (33) by the denominator (8):
33 ÷ 8 = 4 with a remainder of 1
The quotient (4) becomes the whole number part of the mixed number. The remainder (1) becomes the numerator of the fractional part, and the denominator remains the same (8). Therefore, 33/8 as a mixed number is 4 ⅛.
Visualizing the Conversion
Imagine you have 33 slices of pizza, and each pizza has 8 slices. You can make complete pizzas and have some slices left over. You can make 4 complete pizzas (4 x 8 = 32 slices), leaving you with 1 slice remaining. This remaining slice represents the ⅛.
Alternative Methods for Conversion
While the division method is the most straightforward, other methods can help you understand the concept better:
-
Repeated Subtraction: Repeatedly subtract the denominator from the numerator until you get a number smaller than the denominator. The number of times you subtract is the whole number part, and the remaining number is the numerator of the fractional part.
33 - 8 = 25 25 - 8 = 17 17 - 8 = 9 9 - 8 = 1
We subtracted 8 four times, so the whole number is 4. The remainder is 1, giving us 4 ⅛.
-
Using Equivalent Fractions: While less efficient for this specific problem, this method builds a deeper understanding of fractions. You could find an equivalent fraction with a numerator that's easily divisible by the denominator. This method is more helpful with larger numbers.
Why is this Conversion Important?
Converting improper fractions to mixed numbers is crucial for several reasons:
-
Easier Interpretation: Mixed numbers are generally easier to understand and visualize than improper fractions. It's easier to grasp the concept of 4 ⅛ pizzas than 33/8 pizzas.
-
Practical Applications: Many real-world situations require using mixed numbers. Think about measuring ingredients in cooking (1 ½ cups of flour), calculating distances (2 ¾ miles), or working with time (1 ¼ hours).
-
Further Calculations: Mixed numbers are often simpler to work with in addition, subtraction, and even multiplication and division (although conversion to improper fractions is sometimes needed for these).
Practice Problems:
Let's solidify your understanding with a few practice problems:
- Convert 22/5 to a mixed number. (Solution: 4 ⅖)
- Convert 17/4 to a mixed number. (Solution: 4 ¼)
- Convert 35/6 to a mixed number. (Solution: 5 ⅚)
- Convert 49/12 to a mixed number. (Solution: 4 ⅛)
- Convert 61/9 to a mixed number. (Solution: 6 ⁷/₉)
Working with Mixed Numbers: Addition and Subtraction
Adding and subtracting mixed numbers requires a bit more care than adding and subtracting whole numbers. Here's a breakdown:
-
Addition: Add the whole number parts and the fractional parts separately. If the fractional part sums to an improper fraction, convert it to a mixed number and add it to the whole number sum.
-
Subtraction: Similar to addition, subtract the whole numbers and fractions separately. If the fractional part of the subtrahend is larger than the minuend, borrow one from the whole number part, converting it to an improper fraction and adding it to the minuend's fraction.
Example of Adding Mixed Numbers:
2 ¾ + 1 ⅔ = (2 + 1) + (¾ + ⅔) = 3 + (6/12 + 8/12) = 3 + 14/12 = 3 + 1 ⅖ = 4 ⅖
Example of Subtracting Mixed Numbers:
4 ⅛ - 1 ¾ = (Since ¾ > ⅛, we borrow 1 from 4, changing it to 3 and converting 1 into 8/8) = 3 + 8/8 + ⅛ - 1 ¾ = 3 ⁹/₈ - 1 ¾ = (3 - 1) + (⁹/₈ - ⁶/₈) = 2 + 3/8 = 2 ⅜
Converting Mixed Numbers Back to Improper Fractions:
It's often necessary to convert mixed numbers back into improper fractions, especially when performing multiplication and division. Here's how:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Keep the same denominator.
Example:
Convert 4 ⅛ back to an improper fraction:
(4 x 8) + 1 = 33. The improper fraction is 33/8.
Conclusion:
Understanding how to convert between improper fractions and mixed numbers is a cornerstone of arithmetic. The ability to perform these conversions fluently is essential not only for academic success but also for practical applications in everyday life. This guide has provided multiple methods to achieve this conversion, offering a thorough understanding beyond simply memorizing a single formula. By mastering these concepts and practicing the provided problems, you’ll build a strong foundation in fractional arithmetic. Remember, practice is key to mastering any mathematical skill. Consistent work will solidify your understanding and improve your proficiency with fractions.
Latest Posts
Latest Posts
-
35 Is What Percent Of 100
Apr 25, 2025
-
1 Gallon Is How Many Ml
Apr 25, 2025
-
How Do You Divide Fractions With Negative Numbers
Apr 25, 2025
-
What Percent Is 50 Of 250
Apr 25, 2025
-
The Krebs Cycle Occurs In The
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about 33 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.