35 Is What Percent Of 25
Kalali
Apr 14, 2025 · 4 min read
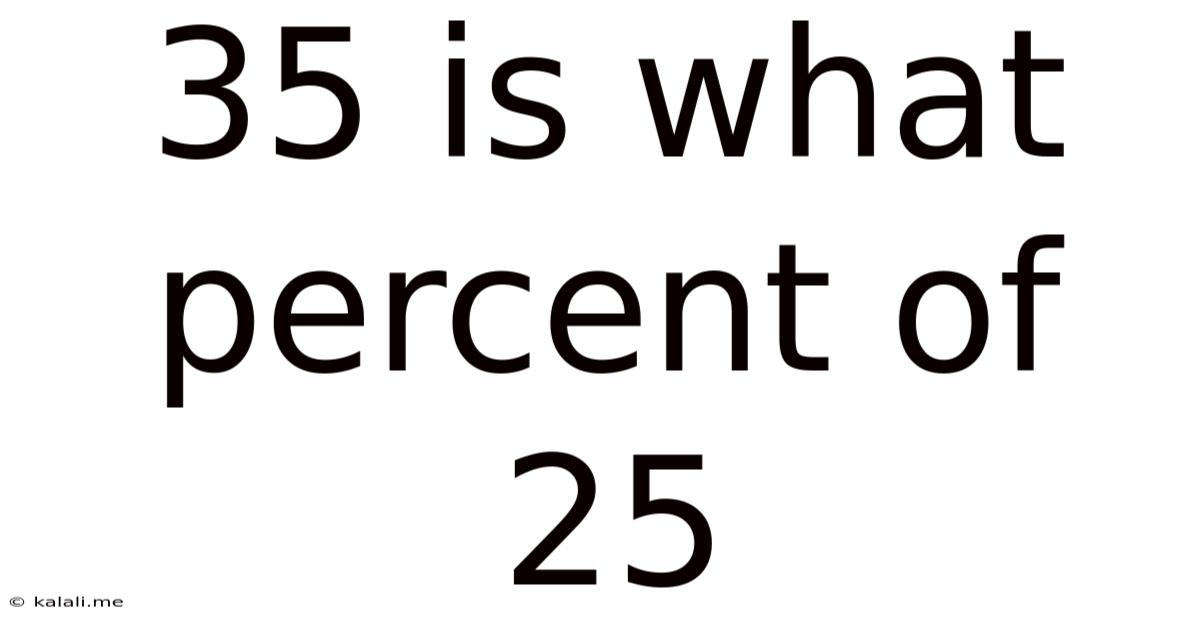
Table of Contents
Decoding Percentages: A Deep Dive into "35 is What Percent of 25?"
This seemingly simple question, "35 is what percent of 25?", unlocks a world of understanding about percentages, their applications, and how to solve them efficiently. While the answer might seem counterintuitive at first glance (because 35 is larger than 25), this problem offers a valuable opportunity to explore the fundamentals of percentage calculations and their broader implications. This article will not only provide the solution but also delve into the underlying concepts, offering practical examples and alternative approaches for similar problems.
Understanding Percentages: The Foundation
Percentages represent a fraction of a whole, expressed as a number out of 100. The term "percent" literally means "per hundred" – a concise way to express proportions. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this basic principle is crucial for solving percentage problems.
Solving "35 is What Percent of 25?"
The question itself frames a classic percentage problem: finding the percentage one number represents of another. Here’s the step-by-step solution:
-
Set up the equation: We can represent the problem as a simple equation:
x% of 25 = 35Where 'x' represents the unknown percentage we need to find.
-
Convert the percentage to a decimal: To make the calculation easier, we convert 'x%' to its decimal equivalent by dividing by 100:
x/100 * 25 = 35 -
Solve for x: Now we can solve for 'x' using algebraic manipulation:
- Multiply both sides by 100:
x * 25 = 3500 - Divide both sides by 25:
x = 3500 / 25 - Calculate the result:
x = 140
- Multiply both sides by 100:
Therefore, 35 is 140% of 25.
Why the Result is Greater Than 100%
The fact that the answer is over 100% might seem unusual at first. This occurs because 35 is larger than 25. A percentage greater than 100% simply indicates that the first number is more than the second number. It's a common occurrence in various real-world applications, such as:
- Percentage increases: If a company's sales increase from 25 units to 35 units, the percentage increase would be 140%.
- Growth rates: In finance, growth rates are often expressed as percentages exceeding 100%.
- Comparative analysis: When comparing two values, one can exceed the other, resulting in a percentage greater than 100%.
Alternative Methods for Solving Percentage Problems
While the algebraic method is efficient, there are alternative approaches for solving percentage problems:
-
Using proportions: You can set up a proportion to solve for the unknown percentage:
x/100 = 35/25Cross-multiply and solve for 'x' to get the same result: 140%.
-
Using a calculator: Most calculators have a percentage function that simplifies the calculation. Simply enter 35 ÷ 25 × 100 to get 140%.
-
Using the formula: The general formula for finding what percentage one number is of another is:
(Part / Whole) * 100 = PercentageIn our case, the part is 35, and the whole is 25.
Real-World Applications of Percentage Calculations
Percentage calculations are fundamental to many aspects of life, including:
- Finance: Calculating interest rates, loan payments, returns on investments, and taxes.
- Business: Determining profit margins, sales growth, market share, and discounts.
- Science: Expressing experimental results, statistical data, and error margins.
- Everyday life: Calculating tips, discounts, sales tax, and many other things.
Expanding on the Problem: Variations and Extensions
Let's explore variations of the problem to further solidify our understanding:
-
"25 is what percent of 35?" This reverses the original problem. Following the same methods, we would find that 25 is approximately 71.43% of 35. This demonstrates the importance of carefully defining which number represents the "part" and which represents the "whole."
-
Finding the value: Instead of finding the percentage, we might be asked: "140% of 25 is what?" In this case, we would simply calculate (140/100) * 25 = 35.
-
Percentage change: We might be asked about the percentage change from 25 to 35. This requires a different calculation:
- Find the difference: 35 - 25 = 10
- Divide the difference by the original value: 10 / 25 = 0.4
- Multiply by 100 to express as a percentage: 0.4 * 100 = 40%
The percentage increase from 25 to 35 is 40%.
-
Complex Scenarios: In real-world scenarios, percentage calculations often involve multiple steps and considerations. For example, calculating a final price after applying multiple discounts or determining the overall impact of several percentage changes.
Conclusion: Mastering Percentage Calculations
Understanding percentages is a vital skill applicable across various disciplines. The question, "35 is what percent of 25?" serves as an excellent example to illustrate the fundamentals of percentage calculations, including setting up equations, solving for unknowns, interpreting results exceeding 100%, and applying different calculation methods. By grasping these concepts and practicing various problem variations, you can confidently tackle more complex percentage problems and apply them to numerous real-world situations. Remember the core principle: percentages are simply fractions expressed as parts of 100, and with a methodical approach, any percentage problem can be solved successfully.
Latest Posts
Latest Posts
-
What Is 8 Out Of 9 As A Percentage
Apr 15, 2025
-
A Bunch Of Amino Acids Attached Together Is Called A
Apr 15, 2025
-
Temperature At Which Water Vapor Condenses
Apr 15, 2025
-
What Is 14 20 As A Percentage
Apr 15, 2025
-
What Percent Of 75 Is 33
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about 35 Is What Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.