35 Is What Percent Of 500
Kalali
Apr 23, 2025 · 5 min read
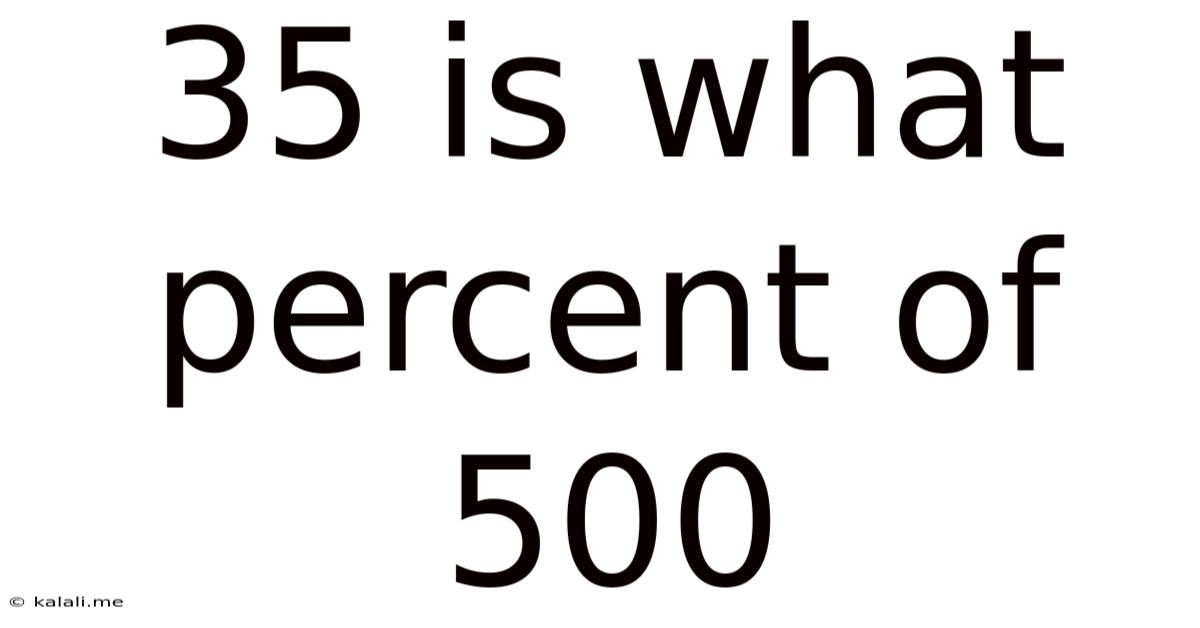
Table of Contents
35 is What Percent of 500? A Comprehensive Guide to Percentage Calculations
This article will delve into the seemingly simple question: "35 is what percent of 500?" While the answer might seem readily apparent, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting to complex financial analysis. We'll not only provide the solution but also explore different methods for solving percentage problems, including the formula approach, the proportion method, and using online calculators. We'll also look at real-world examples and explore advanced percentage concepts. This guide aims to be your complete resource for mastering percentage calculations.
Meta Description: Learn how to calculate percentages with a comprehensive guide that explains how to solve "35 is what percent of 500?" using various methods. Master percentage calculations for everyday use and advanced applications.
Understanding Percentages:
Before diving into the specific problem, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. It represents a portion of a whole. For example, 50% means 50 out of 100, or one-half. Understanding this fundamental concept is key to solving any percentage problem.
Method 1: Using the Percentage Formula
The most straightforward method to determine what percentage 35 represents of 500 is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 35
- Whole: 500
Substituting these values into the formula:
(35 / 500) * 100% = 7%
Therefore, 35 is 7% of 500.
Method 2: The Proportion Method
The proportion method offers another way to solve percentage problems. It involves setting up a proportion, which is an equation stating that two ratios are equal. We can express the problem as a proportion:
35/500 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
35 * 100 = 500 * x
3500 = 500x
x = 3500 / 500
x = 7
Therefore, x = 7%, confirming our previous result.
Method 3: Using Online Calculators
Numerous online percentage calculators are available. Simply input the "part" (35) and the "whole" (500), and the calculator will automatically compute the percentage. These calculators can be particularly helpful for complex percentage problems or when you need quick results. However, understanding the underlying principles is still crucial for interpreting the results and applying the concepts to various situations.
Real-World Applications of Percentage Calculations:
Percentage calculations are ubiquitous in various aspects of daily life and professional settings. Here are a few examples:
-
Calculating Discounts: Retailers frequently offer discounts expressed as percentages. For example, a 20% discount on a $100 item means a reduction of $20 ($100 * 0.20 = $20), leaving a final price of $80.
-
Determining Tax Amounts: Sales taxes are usually calculated as a percentage of the purchase price. Understanding percentage calculations helps determine the final cost of an item, including taxes.
-
Analyzing Financial Statements: Percentage changes are crucial in financial analysis. For instance, comparing year-over-year revenue growth as a percentage reveals the rate of business expansion.
-
Grading Systems: Many educational institutions use percentage grading systems. A student scoring 85 out of 100 on a test achieved an 85% grade.
-
Statistical Analysis: Percentages play a vital role in statistical analysis, such as calculating the percentage of respondents agreeing with a particular survey question. This helps draw meaningful conclusions from the data.
-
Understanding Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Knowing how to calculate percentage helps determine the interest earned or paid.
-
Calculating Tips: Calculating the appropriate tip in a restaurant is usually done by determining a percentage of the total bill.
Advanced Percentage Concepts:
Beyond the basic percentage calculation, let's explore some more advanced concepts:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100%. A positive result indicates an increase, while a negative result signifies a decrease. -
Percentage Points: It's important to distinguish between percentages and percentage points. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original value (10%).
-
Compounding Percentages: Compounding involves calculating percentages on a progressively increasing base. This is common in scenarios like compound interest where interest earned is added to the principal, and subsequent interest is calculated on the higher amount.
-
Percentage of a Percentage: This involves calculating a percentage of another percentage. For example, finding 10% of 25% of a value would involve sequential calculations.
Troubleshooting Common Percentage Errors:
Several common errors can occur when calculating percentages. Here are some crucial points to remember:
-
Confusing Part and Whole: Ensure you correctly identify the part and the whole in your problem.
-
Incorrect Formula Application: Double-check that you use the correct formula and substitute the values accurately.
-
Mathematical Errors: Carefully perform the calculations to avoid simple arithmetic mistakes.
-
Misinterpreting the Results: Understand the context of the percentage and interpret the results appropriately.
Conclusion:
Understanding percentage calculations is a valuable skill applicable across diverse fields. This guide has explored various methods for solving percentage problems, from the basic formula to the proportion method, and emphasized the importance of using online calculators strategically. We have also examined real-world applications and touched upon advanced percentage concepts. By mastering these techniques, you'll be well-equipped to tackle various percentage-related challenges in your personal and professional life. Remember that while calculators offer convenience, a strong grasp of the underlying principles is essential for accurate and insightful calculations. Always double-check your work to avoid common errors. Practice regularly, and you'll soon be proficient in all things percentage.
Latest Posts
Latest Posts
-
What Is 18 Percent Of 100
Apr 23, 2025
-
Whats The Lcm Of 12 And 15
Apr 23, 2025
-
36 Degrees Celsius Is What In Fahrenheit
Apr 23, 2025
-
Is Soil A Substance Or Mixture
Apr 23, 2025
-
How Much Is 40 F In Celsius
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about 35 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.