35 Out Of 50 As A Percentage
Kalali
Mar 10, 2025 · 5 min read
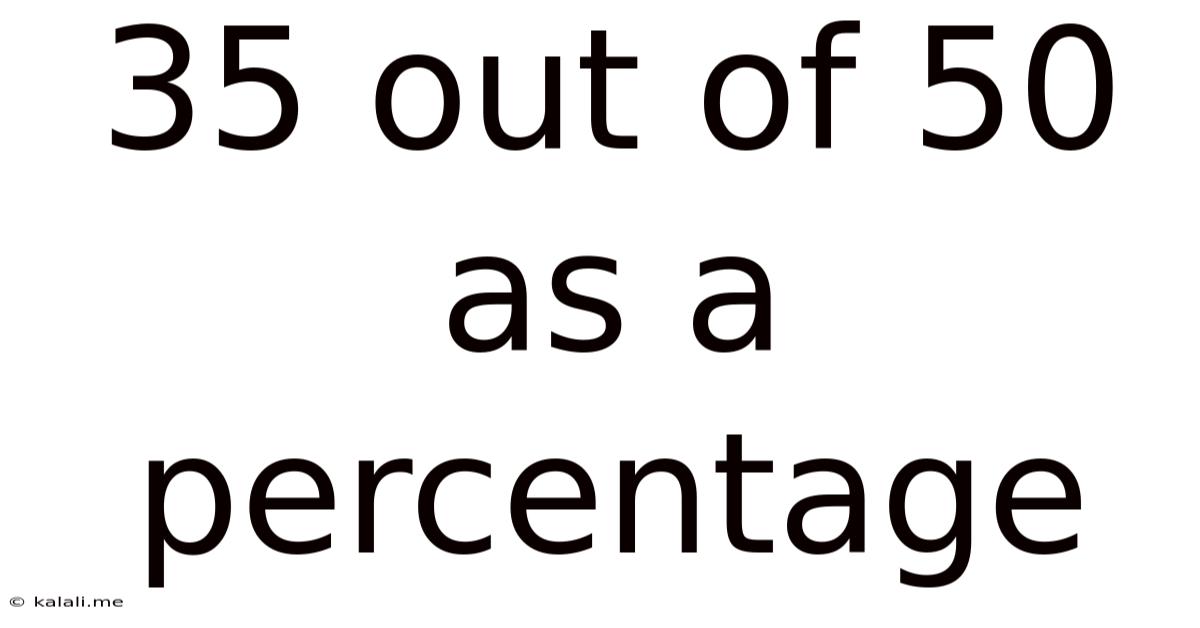
Table of Contents
35 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications, from everyday tasks like calculating discounts and tips to more complex scenarios in finance, statistics, and academic settings. Understanding how to convert fractions to percentages is crucial for effective numerical literacy. This comprehensive guide will delve into how to calculate 35 out of 50 as a percentage, explain the underlying methodology, and provide various real-world examples to solidify your understanding.
Understanding Percentages
Before we dive into the specific calculation, let's establish a firm grasp of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent," meaning "out of 100." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
Calculating 35 out of 50 as a Percentage
To determine what percentage 35 out of 50 represents, we can employ a straightforward method:
1. Express as a Fraction:
First, write the given numbers as a fraction: 35/50. This fraction represents the proportion of 35 out of a total of 50.
2. Convert to a Decimal:
To convert the fraction to a decimal, divide the numerator (35) by the denominator (50):
35 ÷ 50 = 0.7
3. Convert to a Percentage:
Finally, multiply the decimal by 100 to express it as a percentage:
0.7 × 100 = 70%
Therefore, 35 out of 50 is equal to 70%.
Alternative Calculation Methods
While the above method is the most common and straightforward, there are alternative approaches you can use:
1. Using Proportions:
We can set up a proportion:
35/50 = x/100
To solve for x (the percentage), cross-multiply:
50x = 3500
x = 3500/50
x = 70
Therefore, x = 70%, confirming our earlier result.
2. Simplifying the Fraction:
Before converting to a decimal, you can simplify the fraction 35/50. Both the numerator and denominator are divisible by 5:
35 ÷ 5 = 7
50 ÷ 5 = 10
This simplifies the fraction to 7/10. Converting 7/10 to a decimal gives 0.7, which, when multiplied by 100, equals 70%.
This method can be particularly helpful when dealing with larger numbers, making the calculation easier.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world situations:
1. Academic Performance:
Imagine a student scored 35 out of 50 on a test. Understanding that this equates to 70% allows for easy interpretation of their performance relative to the total possible marks. This is crucial for tracking progress and identifying areas for improvement.
2. Financial Calculations:
Percentages are fundamental in finance. For instance, calculating interest rates, discounts, tax rates, and profit margins all require understanding percentage calculations. If a store offers a 30% discount on an item originally priced at $50, you can calculate the discount amount and the final price using percentage calculations.
3. Data Analysis and Statistics:
Percentages are extensively used in data analysis and statistics to represent proportions and trends within datasets. For example, if a survey shows that 35 out of 50 respondents prefer a particular product, the 70% figure provides a clear and concise representation of this preference.
4. Business and Sales:
Businesses utilize percentage calculations to track sales performance, analyze market share, and project future growth. Understanding conversion rates, customer retention rates, and profit margins all rely on accurate percentage calculations.
5. Everyday Life:
Calculating tips in restaurants, understanding sales tax, and determining the percentage increase or decrease in prices all involve practical applications of percentage calculations.
Common Mistakes to Avoid
While calculating percentages is relatively straightforward, certain common mistakes can lead to inaccuracies:
- Incorrect Fraction Formation: Ensure the correct fraction is formed – the part goes in the numerator and the whole goes in the denominator.
- Division Errors: Double-check your division when converting the fraction to a decimal.
- Multiplication Errors: Be cautious when multiplying the decimal by 100 to convert to a percentage.
- Misinterpreting the Result: Always ensure you understand what the calculated percentage represents within the context of the problem.
Advanced Percentage Calculations: Beyond the Basics
While this guide focused on a specific calculation (35 out of 50), the principles extend to more complex scenarios. You might encounter situations where:
- The total is not 100: If you have a score of 35 out of 70, you'll follow the same process, but your final calculation would be 35/70 * 100 = 50%.
- You need to find the original number: If you know a percentage and the resulting amount, you can work backwards to find the original number. For instance, if 70% of a number is 35, you can set up an equation: 0.7x = 35. Solving for x gives you the original number (50).
- You're dealing with percentage increases or decreases: These calculations require understanding how to add or subtract percentages from the original amount.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is essential for navigating various aspects of life, from academic pursuits and financial transactions to professional endeavors and everyday decision-making. By understanding the fundamental principles, practicing different calculation methods, and being mindful of potential errors, you can confidently and accurately calculate percentages in any given context. The ability to translate fractions and decimals into percentages empowers you to interpret data effectively, solve problems efficiently, and make informed decisions based on numerical information. Remember the simple steps: fraction, decimal, percentage, and you'll be well on your way to mastering this vital skill. Regular practice will solidify your understanding and enhance your proficiency in working with percentages, making them an intuitive and indispensable tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
Which Situation Is An Example Of An Internal Conflict
Jul 05, 2025
-
What Year Was I Born If Im 65
Jul 05, 2025
-
Is An Egg A Fruit Or Vegetable
Jul 05, 2025
-
How Many Cups In A Bag Of Chocolate Chips
Jul 05, 2025
-
Spyware Can Result In All Of The Following Except
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 35 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.