36 Is 80 Of What Number
Kalali
Apr 25, 2025 · 5 min read
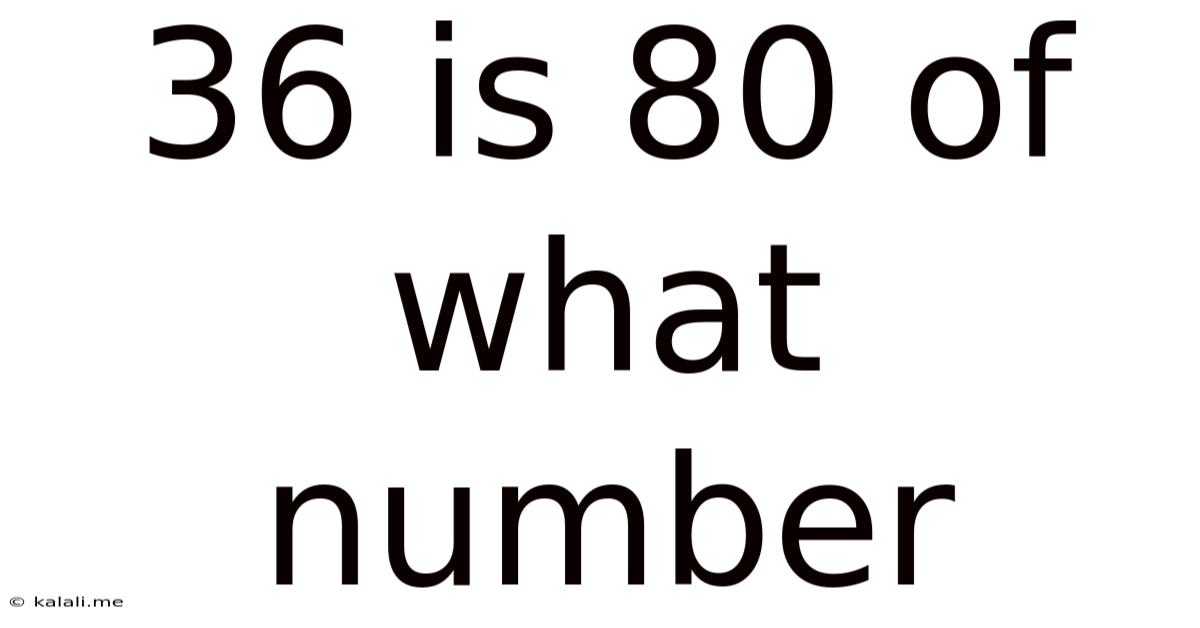
Table of Contents
36 is 80% of What Number? Solving Percentage Problems and Beyond
This seemingly simple question, "36 is 80% of what number?", unlocks a world of practical applications within mathematics and beyond. Understanding how to solve this problem isn't just about finding the answer; it's about grasping the fundamental principles of percentages, proportions, and algebraic reasoning. This comprehensive guide will not only show you how to solve this specific problem but will also equip you with the tools and knowledge to tackle similar percentage-based questions with confidence. We'll delve into various methods, explore real-world applications, and even touch upon advanced concepts related to percentage calculations.
Meta Description: Learn how to solve "36 is 80% of what number?" using multiple methods. This comprehensive guide covers percentages, proportions, algebraic equations, and real-world applications, equipping you with valuable math skills.
Understanding the Problem: Deconstructing Percentages
Before jumping into the solution, let's break down the problem's core components. The phrase "36 is 80% of what number?" represents a proportional relationship. We know one part of the proportion (36) and the percentage (80%), and our goal is to find the whole (the unknown number). This type of problem appears frequently in various fields, from calculating discounts and sales tax to determining grades and analyzing statistical data.
Method 1: Using Algebraic Equations
This is the most common and arguably the most robust method for solving percentage problems. We can translate the statement "36 is 80% of what number?" into an algebraic equation:
36 = 0.80 * x
Where:
- 36 represents the part.
- 0.80 (80% expressed as a decimal) represents the percentage.
- x represents the unknown whole number we are trying to find.
To solve for x, we simply divide both sides of the equation by 0.80:
x = 36 / 0.80
x = 45
Therefore, 36 is 80% of 45.
Method 2: Using Proportions
Proportions offer another effective way to solve this type of problem. We can set up a proportion where one ratio represents the known percentage and the other represents the unknown whole. This method is particularly helpful for visualizing the relationship between the parts and the whole.
The proportion can be set up as follows:
36/x = 80/100
Where:
- 36 is the part.
- x is the whole (unknown).
- 80/100 represents 80% as a fraction.
To solve for x, we cross-multiply:
36 * 100 = 80 * x
3600 = 80x
Divide both sides by 80:
x = 3600 / 80
x = 45
Again, we find that 36 is 80% of 45.
Method 3: The "Is/Of" Method
This is a simplified approach, particularly useful for mental calculations or quick estimations. The "Is/Of" method focuses on the core components of the problem:
- "Is" represents the part. (In our case, 36)
- "Of" represents the whole. (In our case, the unknown x)
- The percentage is expressed as a decimal. (0.80)
We can represent this as:
Part / Whole = Percentage
36 / x = 0.80
Solving for x, we get:
x = 36 / 0.80 = 45
This method provides a streamlined way to directly relate the parts of the problem.
Real-World Applications: Where Percentage Calculations Matter
Understanding how to solve percentage problems extends far beyond the realm of academic exercises. Here are a few examples of real-world applications:
-
Sales and Discounts: Imagine a store offering an 80% discount on an item. If the discounted price is $36, you can use this method to determine the original price.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are all calculated using percentages. Understanding percentage calculations is crucial for managing personal finances effectively.
-
Statistical Analysis: Percentages are used extensively in statistics to represent proportions, frequencies, and probabilities. This is essential in fields like market research, healthcare, and data science.
-
Grades and Assessments: Many academic assessments use percentages to represent a student's performance relative to the total possible score.
-
Tax Calculations: Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to calculate percentages helps in understanding and managing your tax obligations.
Advanced Concepts and Further Exploration
While the problem "36 is 80% of what number?" provides a foundation for understanding percentages, several advanced concepts build upon this understanding:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a key concept in finance and investing.
-
Percentage Change: This measures the relative change between two values. It's crucial in tracking trends, comparing data, and understanding economic growth or decline.
-
Percentage Points: These represent the absolute difference between two percentages. They are often misinterpreted as percentage changes but represent a distinct concept.
-
Weighted Averages: These take into account the relative importance or weight of different values, which are often expressed as percentages.
-
Working with Percentages Above 100%: This scenario signifies growth beyond the original value, commonly used to represent increases in production, population, or investment returns.
Conclusion: Mastering Percentage Calculations
Solving the problem "36 is 80% of what number?" is more than just finding the answer; it's about understanding the underlying principles of percentage calculations and their diverse applications. By mastering these methods – algebraic equations, proportions, and the "is/of" method – you gain a valuable tool applicable across numerous fields. Remember, the core concept lies in understanding the relationship between the part, the whole, and the percentage, enabling you to solve a wide range of problems involving percentages with confidence and efficiency. This understanding forms the foundation for more advanced calculations and analytical skills, opening doors to a deeper appreciation of mathematics and its real-world relevance. From financial planning to data analysis, the ability to work comfortably with percentages is an invaluable asset.
Latest Posts
Latest Posts
-
240 Ml Is How Many Cups
Apr 28, 2025
-
Cuanto Es 168 Centimetros En Pies
Apr 28, 2025
-
A 9 Inch Cube Has A Volume Of
Apr 28, 2025
-
74 Do F Bang Bao Nhieu Do C
Apr 28, 2025
-
10 Mm Is Equal To How Many Inches
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about 36 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.