36 Is What Percent Of 80
Kalali
Apr 18, 2025 · 5 min read
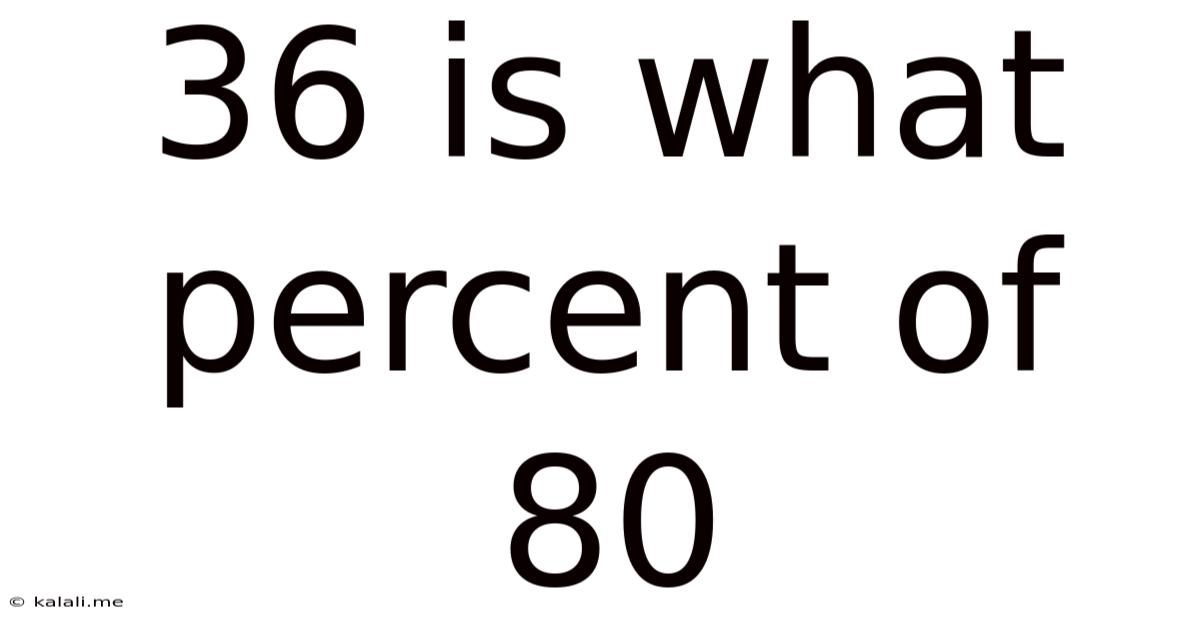
Table of Contents
36 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "36 is what percent of 80?", opens the door to a broader understanding of percentage calculations – a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and analyzing data. This article will not only answer the question directly but will also delve into the underlying concepts, provide multiple methods for solving similar problems, and explore practical applications of percentage calculations.
Meta Description: Learn how to calculate percentages with this comprehensive guide. We'll solve "36 is what percent of 80?" and explore different methods, practical applications, and real-world examples to master percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (Latin: per centum). Therefore, 1% represents 1/100, 50% represents 50/100 (or 1/2), and 100% represents 100/100 (or 1). Percentages are a useful tool because they allow us to compare proportions easily and understand relative quantities.
Method 1: Using the Formula
The most straightforward method to solve "36 is what percent of 80?" involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 36 (the number we're considering as a portion of the whole)
- Whole: 80 (the total amount)
Substituting these values into the formula:
(36 / 80) * 100% = 45%
Therefore, 36 is 45% of 80.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion:
x / 100 = 36 / 80
Where 'x' represents the percentage we need to find. To solve for 'x', we cross-multiply:
80x = 3600
Then, divide both sides by 80:
x = 3600 / 80 = 45
Therefore, x = 45%, confirming our previous result. This method is particularly helpful in visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
This method involves converting the fraction (Part/Whole) into a decimal and then multiplying by 100%:
- Convert the fraction to a decimal: 36 / 80 = 0.45
- Multiply by 100%: 0.45 * 100% = 45%
This method highlights the connection between decimals and percentages, demonstrating that a decimal can be easily converted to a percentage by multiplying by 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many aspects of life:
-
Finance: Calculating interest rates, discounts, profit margins, sales tax, and investment returns all rely heavily on percentage calculations. For example, determining the final price of an item after a 20% discount requires calculating the percentage of the discount and subtracting it from the original price. Similarly, understanding compound interest involves repeated percentage calculations over time.
-
Statistics: Percentages are essential for interpreting data, representing proportions within datasets, and communicating findings effectively. For example, analyzing survey results often involves expressing responses as percentages of the total number of respondents. This allows for easier comparison and interpretation of trends.
-
Science: Percentage calculations are used extensively in various scientific fields. For instance, calculating the percentage of a certain element in a compound, or the percentage change in a biological population, requires a strong understanding of percentage calculations.
-
Everyday Life: Calculating tips in restaurants, determining the percentage of a specific ingredient in a recipe, or understanding sale prices all involve the application of percentage calculations. These seemingly minor applications highlight the pervasive nature of percentage calculations in our daily lives.
Advanced Percentage Problems and Variations
While "36 is what percent of 80?" is a relatively straightforward problem, percentage calculations can become more complex. Here are some variations:
-
Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, "45% of what number is 36?" This requires rearranging the formula to solve for the "Whole".
-
Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, "What is 45% of 80?" This involves multiplying the percentage (as a decimal) by the whole.
-
Percentage Increase/Decrease: Calculating percentage changes requires understanding the difference between the initial and final values, dividing by the initial value, and multiplying by 100%. For example, if a price increases from $80 to $100, the percentage increase is calculated as follows: [(100-80)/80] * 100% = 25%.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The more you practice, the more comfortable and proficient you will become with percentage calculations.
-
Use Multiple Methods: Trying different methods for solving percentage problems helps solidify your understanding and allows you to choose the most efficient approach for different situations.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages and their relationship to fractions and decimals.
-
Break Down Complex Problems: If faced with a complex percentage problem, break it down into smaller, manageable steps.
-
Utilize Online Resources: Numerous online calculators and tutorials can assist in learning and practicing percentage calculations. However, always aim to understand the methodology behind the calculations, rather than just relying on the calculator's output.
Conclusion
The question, "36 is what percent of 80?" serves as a springboard for exploring the versatile world of percentage calculations. Mastering this fundamental skill is essential for success in various academic, professional, and personal endeavors. By understanding the different methods, appreciating their practical applications, and consistently practicing, you can confidently tackle percentage problems of any complexity and apply this valuable skill to numerous real-world situations. Remember, the key is not just to find the answer (45%), but to understand how to find the answer and the underlying principles that govern percentage calculations.
Latest Posts
Latest Posts
-
Least Common Multiple 4 And 8
Apr 22, 2025
-
How Many Hours Is 205 Minutes
Apr 22, 2025
-
What Is 85 Degrees In Celsius
Apr 22, 2025
-
What Percentage Is 7 Out Of 10
Apr 22, 2025
-
Convert 59 Degrees Fahrenheit To Celsius
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 36 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.