36 Out Of 45 As A Percentage
Kalali
Apr 12, 2025 · 5 min read
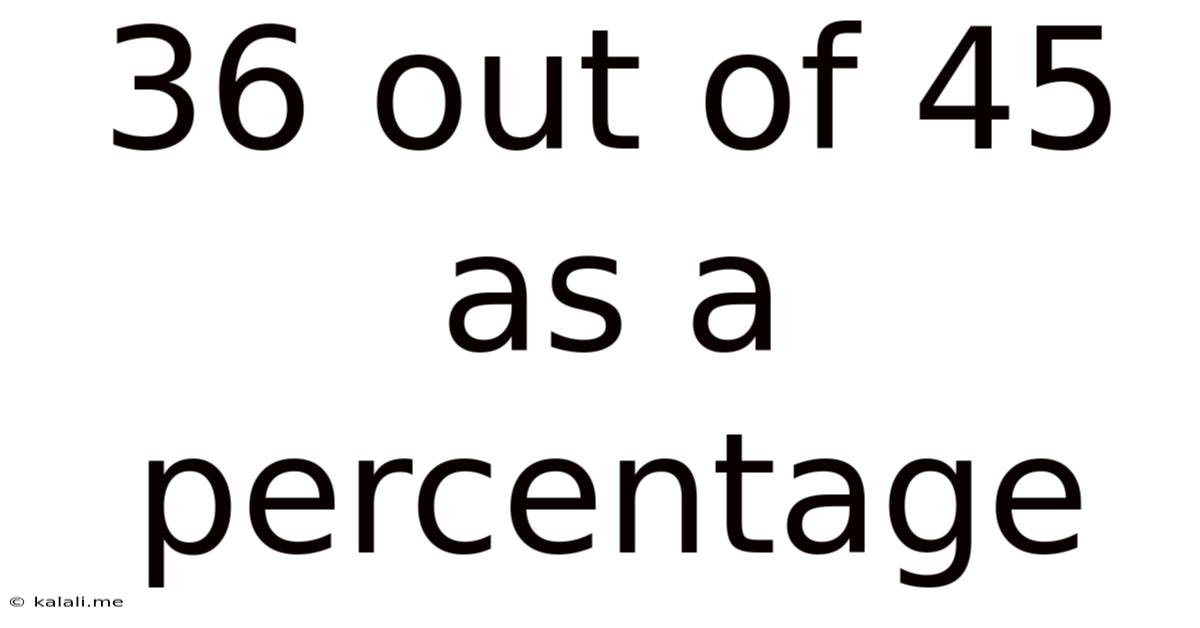
Table of Contents
36 out of 45 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex statistical analyses and scientific research. Understanding how to convert fractions and ratios into percentages allows for easier comparison and interpretation of data. This article delves into the specific calculation of 36 out of 45 as a percentage, providing a step-by-step guide and exploring various methods to solve this type of problem, including practical applications and potential real-world scenarios. We will also touch upon the broader context of percentage calculations and their importance.
Understanding Percentages: A Quick Recap
A percentage represents a fraction of 100. It expresses a proportion or ratio as a number out of 100. The symbol "%" is used to denote percentages. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Classic Fraction-to-Percentage Conversion
The most straightforward way to calculate 36 out of 45 as a percentage is to express it as a fraction and then convert it to a percentage.
-
Express as a Fraction: "36 out of 45" can be written as the fraction 36/45.
-
Simplify the Fraction (Optional but Recommended): Before converting to a percentage, simplifying the fraction makes the calculation easier. Both 36 and 45 are divisible by 9:
36 ÷ 9 = 4 45 ÷ 9 = 5
Therefore, 36/45 simplifies to 4/5.
-
Convert to a Decimal: To convert the fraction to a percentage, divide the numerator (top number) by the denominator (bottom number):
4 ÷ 5 = 0.8
-
Convert Decimal to Percentage: Multiply the decimal by 100 and add the percentage symbol (%):
0.8 x 100 = 80%
Therefore, 36 out of 45 is equal to 80%.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where x represents the percentage we want to find:
36/45 = x/100
To solve for x, cross-multiply:
45x = 3600
Divide both sides by 45:
x = 3600/45 = 80
Therefore, x = 80%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 36 ÷ 45 and then multiply the result by 100. The calculator will directly provide the answer: 80%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life and professional settings. Here are some examples:
-
Academic Performance: If a student answers 36 out of 45 questions correctly on a test, their score is 80%. This helps evaluate their understanding of the subject matter. This is a prime example of how calculating "36 out of 45 as a percentage" applies directly.
-
Sales and Discounts: Stores often advertise discounts as percentages. For instance, a "20% off" sale means you pay 80% of the original price. Calculating percentages helps determine the final price after a discount. Understanding this principle is critical for consumers making informed purchasing decisions.
-
Financial Calculations: Percentage calculations are fundamental in finance. Calculating interest rates, returns on investments, tax rates, and profit margins all involve percentage calculations. This is important for understanding personal finances and managing investments.
-
Statistical Analysis: Percentages are widely used in data analysis and research to represent proportions within datasets. For example, determining the percentage of respondents who favor a particular product in a survey requires percentage calculations. This is especially crucial in providing actionable insights from market research and other data-driven fields.
-
Scientific Research: Percentage calculations are essential for reporting and interpreting results in various scientific fields, such as chemistry, physics, and biology. For example, calculating the percentage yield of a chemical reaction or the percentage of a population with a specific trait relies on accurate percentage calculations.
Beyond the Basic Calculation: Exploring Related Concepts
While calculating 36 out of 45 as a percentage is a straightforward process, understanding related concepts strengthens your grasp of percentages.
-
Percentage Increase and Decrease: These calculations determine the change in a value relative to its initial value. For example, if a product's price increases from $50 to $60, the percentage increase is 20%. Conversely, a decrease from $60 to $50 represents a 16.7% decrease. These are essential for analyzing trends and growth.
-
Percentage Points: It's crucial to differentiate between percentage points and percentage changes. A change from 40% to 50% is a 10 percentage point increase, but a 25% increase in the percentage itself. This distinction is vital for clarity in interpreting statistical data and reporting changes.
-
Compounding Percentages: Compounding refers to earning interest on both the principal amount and accumulated interest. Understanding compound interest is vital for financial planning, especially for long-term investments and loans. This concept highlights the power of exponential growth.
Advanced Applications and Considerations
-
Weighted Averages: In scenarios where different values hold varying weights, weighted averages are used. This is common in academic grading where different assignments or exams carry different weights towards the final grade.
-
Percentage Change Over Multiple Periods: Calculating percentage changes over multiple time periods requires careful consideration to avoid compounding errors. The correct method depends on the specific application.
Conclusion
Calculating 36 out of 45 as a percentage—which equals 80%—is a fundamental skill with wide-ranging applications. Mastering percentage calculations empowers you to interpret data, make informed decisions, and excel in various fields. This article provided various methods for performing this calculation and explored its relevance in diverse real-world contexts. A strong understanding of percentages, beyond the simple calculation, opens up a broader world of mathematical and analytical possibilities. Furthermore, remembering the different methods and their subtle nuances makes you more versatile in your problem-solving approach, ultimately refining your quantitative skills.
Latest Posts
Latest Posts
-
How Does Metamorphic Rock Become Igneous Rock
Apr 18, 2025
-
What Is The Opposite Of Photosynthesis
Apr 18, 2025
-
How Many Inches Is 171 Cm
Apr 18, 2025
-
30 Meters Is How Many Yards
Apr 18, 2025
-
What Is 1 Percent Of A Million
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about 36 Out Of 45 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.