37 4 As A Mixed Number
Kalali
Apr 10, 2025 · 5 min read
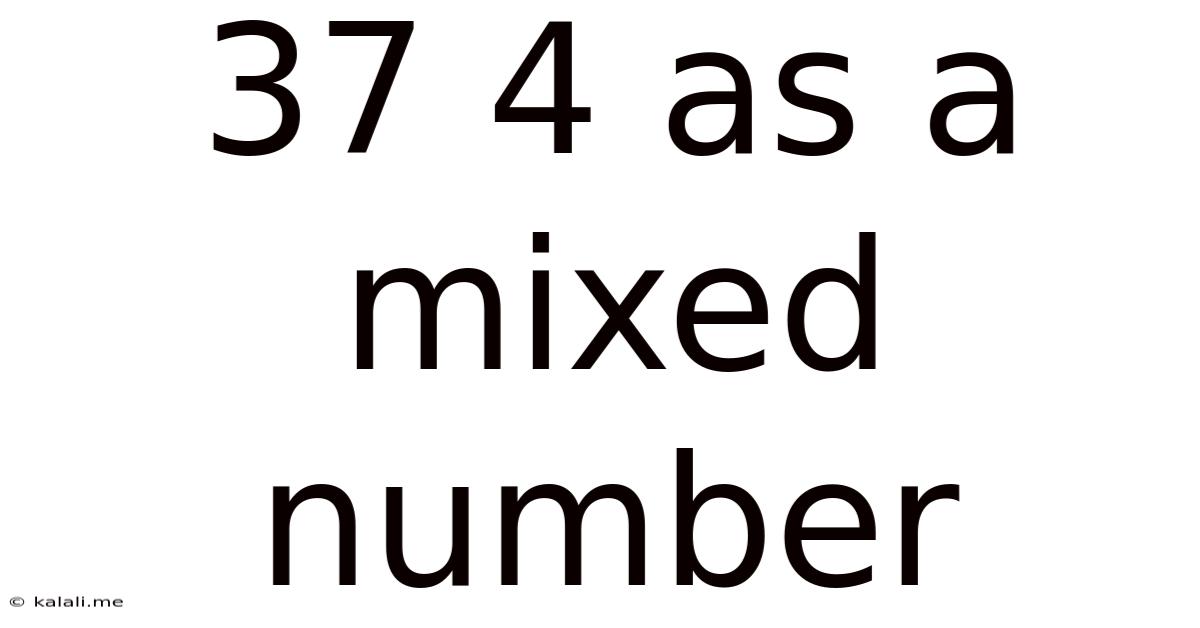
Table of Contents
37/4 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 37/4 into a mixed number, explaining the concept in detail and providing practical examples to solidify your understanding. We'll also explore related concepts and offer tips for tackling similar problems. This article aims to be a complete resource, helpful for students, educators, and anyone looking to brush up on their fraction skills.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that's greater than one whole unit.
Why Convert Improper Fractions to Mixed Numbers?
Improper fractions, like 37/4, have a numerator that is larger than or equal to the denominator. While perfectly valid mathematically, they are often less intuitive to understand than mixed numbers. Mixed numbers offer a clearer representation of the quantity, making them easier to visualize and use in real-world applications, like measuring ingredients in a recipe or calculating distances.
Converting 37/4 to a Mixed Number: Step-by-Step
The process of converting an improper fraction to a mixed number involves division. Here's how to convert 37/4:
-
Divide the numerator by the denominator: Divide 37 by 4.
37 ÷ 4 = 9 with a remainder of 1
-
The quotient becomes the whole number: The quotient (the result of the division) is 9. This becomes the whole number part of our mixed number.
-
The remainder becomes the numerator: The remainder (the number left over after the division) is 1. This becomes the numerator of the fractional part of our mixed number.
-
The denominator stays the same: The denominator remains unchanged from the original improper fraction. It remains 4.
-
Combine the whole number and the fraction: Combine the whole number and the fraction to form the mixed number.
Therefore, 37/4 as a mixed number is 9 1/4.
Visualizing the Conversion
Imagine you have 37 quarters. A quarter is 1/4 of a dollar. How many dollars do you have?
You can group the quarters into sets of four (because four quarters make a dollar). You can make nine complete sets of four quarters, leaving you with one quarter remaining. This translates directly to 9 1/4 dollars, mirroring our calculation above.
Practice Problems: Similar Conversions
Let's solidify our understanding by converting other improper fractions to mixed numbers using the same method:
-
47/5: 47 ÷ 5 = 9 with a remainder of 2. Therefore, 47/5 = 9 2/5.
-
26/3: 26 ÷ 3 = 8 with a remainder of 2. Therefore, 26/3 = 8 2/3.
-
61/8: 61 ÷ 8 = 7 with a remainder of 5. Therefore, 61/8 = 7 5/8.
-
100/7: 100 ÷ 7 = 14 with a remainder of 2. Therefore, 100/7 = 14 2/7.
Converting Mixed Numbers back to Improper Fractions
It's also crucial to understand the reverse process – converting a mixed number back into an improper fraction. This is essential for performing calculations involving mixed numbers. Here's how:
-
Multiply the whole number by the denominator: Multiply the whole number part of the mixed number by the denominator of the fraction.
-
Add the numerator: Add the result from step 1 to the numerator of the fraction.
-
Keep the denominator the same: The denominator remains the same as in the original mixed number.
Let's convert 9 1/4 back to an improper fraction:
-
9 (whole number) * 4 (denominator) = 36
-
36 + 1 (numerator) = 37
-
The denominator remains 4.
Therefore, 9 1/4 = 37/4.
Real-World Applications of Mixed Numbers
Mixed numbers frequently appear in everyday situations:
-
Cooking: Recipes often call for mixed numbers of cups or tablespoons of ingredients (e.g., 2 ½ cups of flour).
-
Measurement: Measuring lengths, weights, or volumes often results in mixed numbers (e.g., 5 3/8 inches).
-
Time: Time is often expressed using mixed numbers (e.g., 1 ½ hours).
Advanced Concepts and Further Exploration
Once you master converting between improper fractions and mixed numbers, you can delve into more complex mathematical operations involving fractions, such as:
-
Adding and subtracting mixed numbers: Requires converting to improper fractions, performing the operation, and then converting back to a mixed number.
-
Multiplying and dividing mixed numbers: Similar to addition and subtraction, converting to improper fractions simplifies the process.
-
Working with decimals and fractions: Understanding how to convert between fractions and decimals expands your mathematical toolkit.
Conclusion
Converting improper fractions to mixed numbers is a vital skill in mathematics. This guide provides a detailed, step-by-step approach, supplemented with practice problems and real-world examples. Mastering this skill will not only improve your understanding of fractions but also equip you to tackle more advanced mathematical concepts with confidence. Remember to practice regularly, and don't hesitate to explore further resources to deepen your understanding of fractions and their applications. Through consistent practice and a clear understanding of the underlying principles, you'll find that working with fractions, including converting improper fractions like 37/4 to mixed numbers, becomes increasingly straightforward and intuitive.
Latest Posts
Latest Posts
-
What Episode Does Ichigo Get His Powers Back
Jul 05, 2025
-
Pokemon Mystery Dungeon Red Rescue Team Codes
Jul 05, 2025
-
How Much Is 25 20 Dollar Bills
Jul 05, 2025
-
How Many Apples In 3 Lb Bag
Jul 05, 2025
-
What Is Half A Quarter Of 400
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about 37 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.