38 Is What Percent Of 50
Kalali
Apr 22, 2025 · 5 min read
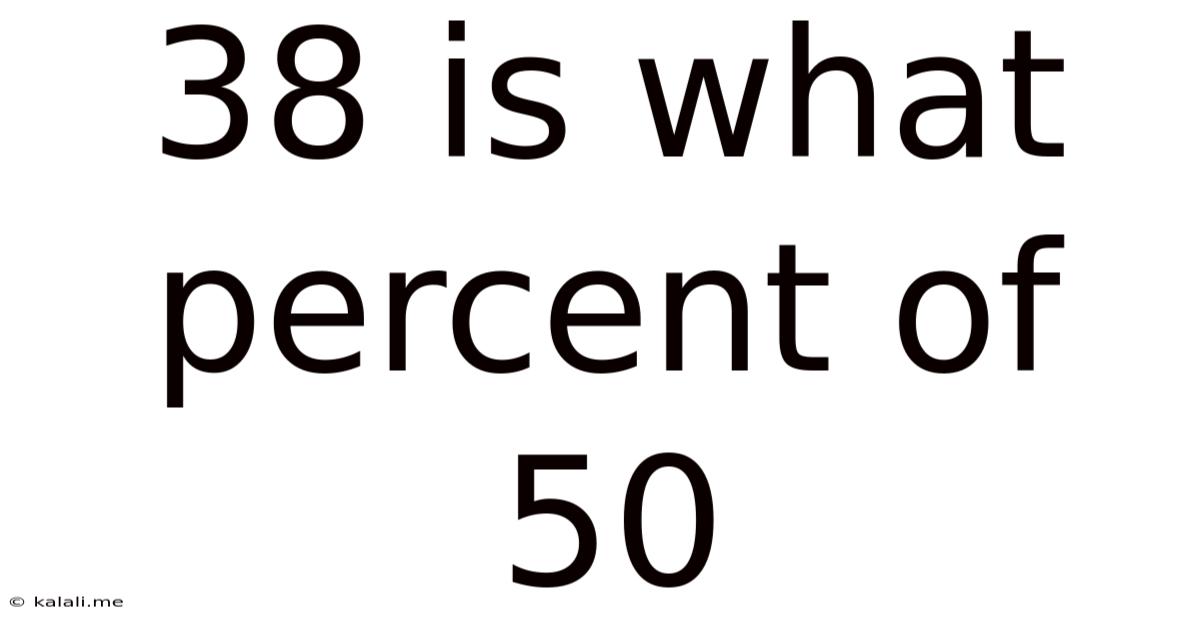
Table of Contents
38 is What Percent of 50? A Deep Dive into Percentage Calculations and Their Applications
Meta Description: Learn how to calculate percentages, understand the concept of "38 is what percent of 50?", and explore diverse applications of percentage calculations in everyday life, business, and beyond. This comprehensive guide covers the basics and delves into advanced percentage problems.
Calculating percentages is a fundamental skill applicable across numerous fields, from simple everyday tasks to complex financial analyses. Understanding how to perform these calculations efficiently and accurately is crucial for anyone seeking numerical literacy. This article tackles the specific question, "38 is what percent of 50?", but expands significantly to provide a comprehensive understanding of percentage calculations and their real-world applications.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (Latin: per centum). Percentages are a convenient way to represent proportions and make comparisons. For instance, scoring 80% on a test means you answered 80 out of 100 questions correctly. This is easily understood and readily comparable to other scores expressed as percentages.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part: Represents the specific portion you're interested in.
- Whole: Represents the total amount.
- Percentage: The result expressed as a number out of 100.
Solving "38 is What Percent of 50?"
Now, let's apply this formula to answer the question posed in the title: "38 is what percent of 50?".
Here, 38 is the part, and 50 is the whole. Substituting these values into the formula:
(38 / 50) * 100 = Percentage
(0.76) * 100 = 76
Therefore, 38 is 76% of 50.
Beyond the Basics: Different Approaches and Scenarios
While the above method is straightforward, let's explore other approaches to solve percentage problems and consider different scenarios.
Method 1: Using Proportions
Percentage problems can also be solved using proportions. We can set up a proportion:
38/50 = x/100
Where 'x' represents the percentage we want to find. Cross-multiplying, we get:
50x = 3800
x = 3800/50
x = 76
Again, this confirms that 38 is 76% of 50.
Method 2: Working with Decimals
Instead of directly using the percentage formula, we can first convert the fraction to a decimal and then multiply by 100:
38/50 = 0.76
0.76 * 100 = 76%
This approach is particularly useful when dealing with more complex calculations or when using calculators.
Scenario 1: Finding the Part
Let's reverse the problem. If we know the percentage and the whole, how do we find the part?
For example, what is 20% of 80?
We can use the formula:
(Percentage/100) * Whole = Part
(20/100) * 80 = 16
Therefore, 20% of 80 is 16.
Scenario 2: Finding the Whole
Similarly, if we know the part and the percentage, we can find the whole.
For example, if 15 is 30% of a certain number, what is that number?
We can rearrange the formula:
Whole = (Part / Percentage) * 100
Whole = (15 / 30) * 100 = 50
Therefore, 15 is 30% of 50.
Real-World Applications of Percentage Calculations
Percentage calculations are pervasive in various aspects of daily life and professional fields. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses. Understanding percentage changes in stock prices or investment returns is crucial for informed financial decision-making. Calculating loan repayments and compound interest also heavily relies on percentage calculations.
-
Retail and Sales: Determining discounts (e.g., a 25% off sale), calculating sales tax, and analyzing profit margins are essential for businesses. Understanding markups and price reductions expressed as percentages is crucial for both consumers and businesses.
-
Science and Statistics: Percentages are used extensively in data representation and analysis. Statistical measures like percentages of success or failure rates, error margins, and confidence intervals are fundamental to research and interpretation of data.
-
Education: Grading systems often utilize percentages to represent student performance. Analyzing test scores, class averages, and individual progress all involve percentage calculations.
-
Everyday Life: Calculating tips at restaurants, figuring out sale prices, understanding nutritional information (e.g., percentage of daily value), and interpreting survey results are everyday instances where percentage calculations are beneficial.
Advanced Percentage Problems and Techniques
Beyond the basic calculations, percentage problems can become more complex. For instance:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding how to determine the difference and express it as a percentage of the original value.
-
Successive Percentages: Applying multiple percentages sequentially (e.g., a 10% discount followed by a 5% discount) requires careful calculation to avoid errors. It's important to remember that these discounts don't simply add up.
-
Compound Interest: Calculating compound interest involves repeatedly applying a percentage to a growing principal amount. This concept is fundamental to understanding long-term investments and loan repayments.
-
Percentage Points: It's important to differentiate between percentage points and percentage changes. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the initial 10%.
Mastering these advanced concepts requires a solid grasp of the fundamental principles and a systematic approach to problem-solving.
Conclusion: The Importance of Percentage Mastery
The ability to calculate and understand percentages is a crucial skill for navigating the complexities of modern life. From managing personal finances to interpreting data and making informed decisions in various professional settings, a strong understanding of percentages empowers individuals to make better choices and become more numerically literate. While seemingly simple, the applications of percentage calculations are vast and profound, making it a vital skill to hone and practice. Understanding the different methods and their applications, as explored in this article, provides a strong foundation for tackling a wide range of percentage-related problems.
Latest Posts
Latest Posts
-
300 Cm To Inches To Feet
Apr 22, 2025
-
What Are The Multiples Of 25
Apr 22, 2025
-
How Many Inches Is 270 Cm
Apr 22, 2025
-
Lowest Common Multiple Of 24 And 40
Apr 22, 2025
-
How Much Is 110 Cm In Inches
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about 38 Is What Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.