4 And 1/2 As A Decimal
Kalali
Apr 03, 2025 · 5 min read
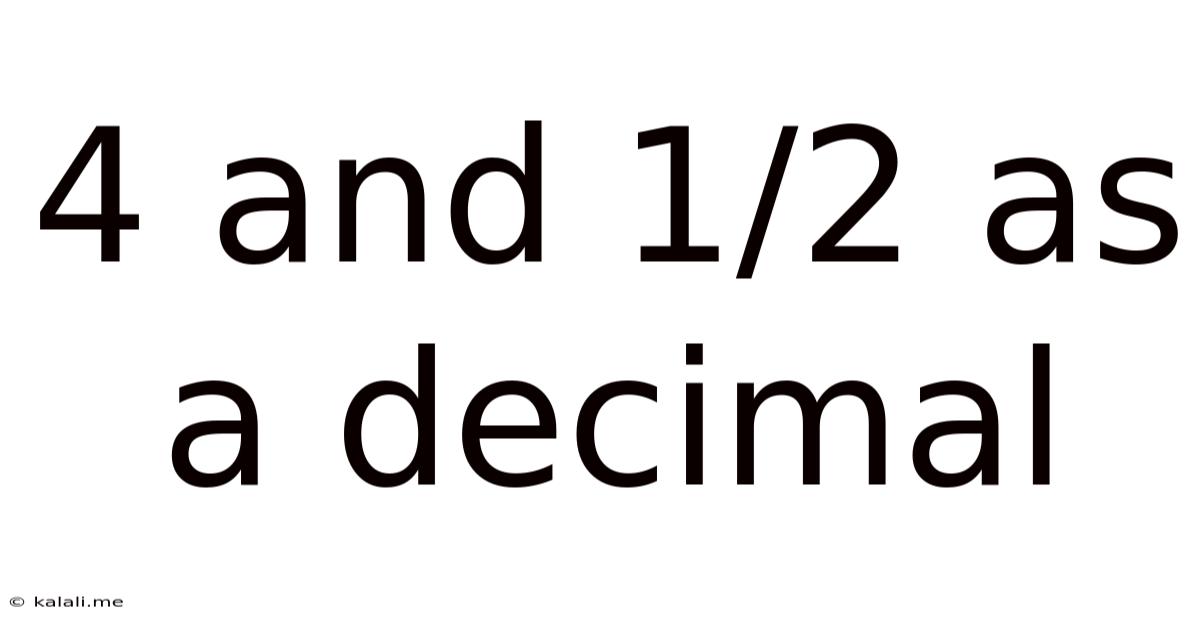
Table of Contents
4 and 1/2 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This comprehensive guide delves into the conversion of the mixed number 4 and 1/2 into its decimal representation, exploring the underlying principles and providing practical examples. We'll also touch upon the broader context of fraction-to-decimal conversions and their significance.
Understanding Fractions and Decimals
Before diving into the conversion of 4 and 1/2, let's solidify our understanding of fractions and decimals.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one of two equal parts.
Decimals: A decimal is a way of expressing a number that is not a whole number using a base-ten system. The decimal point separates the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For instance, 0.5 represents five-tenths, or 5/10.
Mixed Numbers: A mixed number combines a whole number and a fraction. 4 and 1/2 is a mixed number, representing four whole units and one-half of another unit.
Converting 4 and 1/2 to a Decimal
There are several ways to convert 4 and 1/2 into its decimal equivalent:
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This is perhaps the most straightforward approach. We first convert the fraction 1/2 into its decimal form. Since 1/2 represents one out of two equal parts, and 2 goes into 10 five times, it can be written as 0.5. Now, we add the whole number 4:
4 + 0.5 = 4.5
Therefore, 4 and 1/2 as a decimal is 4.5.
Method 2: Converting the Mixed Number to an Improper Fraction and then to a Decimal
This method involves first converting the mixed number into an improper fraction. An improper fraction has a numerator that is greater than or equal to its denominator. To do this, we multiply the whole number (4) by the denominator (2) and add the numerator (1):
(4 * 2) + 1 = 9
This gives us a numerator of 9. The denominator remains the same (2), resulting in the improper fraction 9/2.
Now, we divide the numerator (9) by the denominator (2):
9 ÷ 2 = 4.5
Again, we arrive at the decimal equivalent of 4.5.
Real-World Applications of Decimal Conversions
The ability to convert fractions to decimals is crucial in various real-world situations:
-
Finance: Calculating percentages, interest rates, and discounts often involves working with both fractions and decimals. Understanding their interrelationship is essential for accurate financial calculations. For example, calculating a 50% discount (which is equivalent to 1/2) on a $10 item requires converting 1/2 to 0.5 and then multiplying by $10.
-
Measurement: Many measurement systems use both fractions and decimals. Converting between the two is important for accuracy and consistency. For example, in construction or engineering, measurements might be given in inches (e.g., 4 1/2 inches) and then need to be converted to decimal feet (e.g., 3.75 feet) for calculations.
-
Data Analysis: In statistics and data analysis, dealing with both fractional and decimal data is common. Converting between the two facilitates calculations and data interpretation. Averages, percentages, and other statistical metrics might involve converting fractions to decimals for easier computation.
-
Cooking and Baking: Recipes often use fractions (e.g., 1/2 cup of sugar) but some kitchen scales display measurements in decimals. Converting between fractions and decimals ensures accurate ingredient measurements.
-
Programming and Computer Science: Many programming languages and computer applications require numerical input in decimal format. Converting fractions to decimals is often a necessary step in translating real-world problems into code.
Further Exploring Fraction-to-Decimal Conversions
Beyond 4 and 1/2, the principle of converting fractions to decimals remains the same. The key is to divide the numerator by the denominator. However, some fractions yield terminating decimals (like 1/2 = 0.5), while others yield repeating decimals (like 1/3 = 0.333...).
Terminating Decimals: These are decimals that have a finite number of digits after the decimal point. They result from fractions where the denominator can be expressed as a power of 10 (e.g., 10, 100, 1000) or has only prime factors of 2 and/or 5.
Repeating Decimals: These are decimals where one or more digits repeat infinitely after the decimal point. They arise from fractions whose denominators contain prime factors other than 2 and 5. Repeating decimals are often represented using a bar over the repeating digits (e.g., 1/3 = 0.3̅).
Understanding the difference between terminating and repeating decimals provides a more complete understanding of fraction-to-decimal conversions.
Advanced Concepts and Applications
The seemingly simple conversion of 4 and 1/2 to 4.5 opens doors to more advanced mathematical concepts:
-
Significant Figures and Rounding: When dealing with decimal approximations, especially from repeating decimals, the concept of significant figures and rounding becomes crucial for accuracy and clarity. Understanding how to round decimals appropriately is essential in various fields, especially science and engineering.
-
Scientific Notation: For extremely large or small numbers, scientific notation is used. This notation involves expressing numbers as a product of a number between 1 and 10 and a power of 10. Converting fractions to decimals often becomes a preliminary step before applying scientific notation.
-
Binary and Other Number Systems: While our discussion focuses on the decimal system (base-10), computers and other digital systems utilize binary (base-2) and other number systems. Understanding how fractions and decimals translate across different number systems is important in computer science and related fields.
Conclusion
The conversion of 4 and 1/2 to its decimal equivalent, 4.5, may seem trivial at first glance. However, this simple conversion exemplifies a fundamental mathematical concept with wide-ranging applications. Understanding fractions, decimals, and the techniques for converting between them is essential for success in various academic and professional pursuits. From financial calculations and measurement to data analysis and programming, the ability to work confidently with fractions and decimals is a valuable skill that extends far beyond the classroom. By mastering these concepts, individuals can enhance their problem-solving capabilities and navigate the numerical world with increased precision and understanding.
Latest Posts
Latest Posts
-
What Is 1 1 4 In Mm
Apr 04, 2025
-
14 C Is What In Fahrenheit
Apr 04, 2025
-
How Many Feet In 90 Inches
Apr 04, 2025
-
How Many Inches Is 90 Centimeters
Apr 04, 2025
-
How Much Is 25 Degrees Fahrenheit In Celsius
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 4 And 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
