4 Divided By 6 As A Fraction
Kalali
Jul 25, 2025 · 6 min read
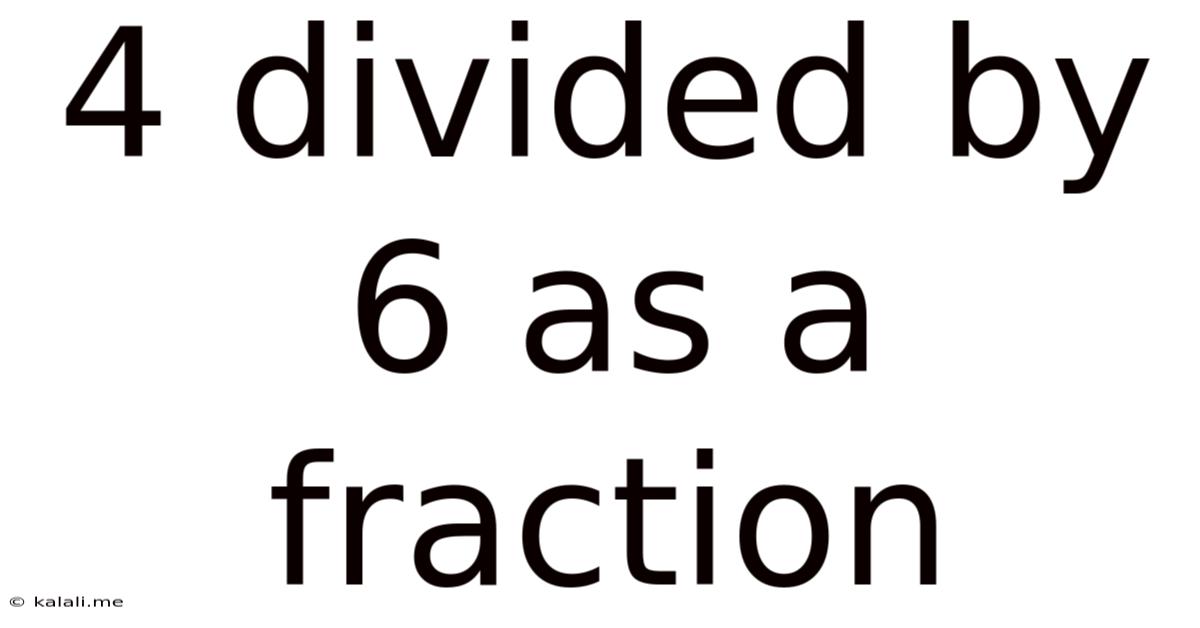
Table of Contents
4 Divided by 6 as a Fraction: A Comprehensive Guide
Meta Description: Learn how to express 4 divided by 6 as a fraction, simplifying it to its lowest terms. This comprehensive guide covers the fundamentals of division, fractions, and simplification, including real-world examples and practice problems. Understand the concept thoroughly and master this essential mathematical skill.
Dividing numbers is a fundamental arithmetic operation, and expressing the result as a fraction is a key aspect of mathematical understanding. This in-depth guide will explore the process of expressing 4 divided by 6 as a fraction, encompassing the underlying principles and demonstrating how to simplify the fraction to its lowest terms. We'll also delve into related concepts and provide practical examples to solidify your understanding.
Understanding Division and Fractions
Before we dive into the specifics of 4 divided by 6, let's refresh our understanding of division and fractions.
Division is the process of splitting a number into equal parts. For instance, dividing 12 by 3 means splitting 12 into 3 equal groups, with each group containing 4. This can be represented as 12 ÷ 3 = 4.
A fraction represents a part of a whole. It consists of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of equal parts the whole is divided into. For example, the fraction ¾ means we have 3 parts out of a total of 4 equal parts.
Expressing 4 Divided by 6 as a Fraction
To express 4 divided by 6 as a fraction, we simply write the dividend (the number being divided) as the numerator and the divisor (the number we're dividing by) as the denominator. Therefore, 4 divided by 6 is written as:
4/6
This fraction represents 4 out of 6 equal parts. Imagine you have 6 slices of pizza, and you eat 4 of them. The fraction 4/6 represents the portion of the pizza you consumed.
Simplifying Fractions
The fraction 4/6 is not in its simplest form. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and denominator and divide both by it.
The GCD of 4 and 6 is 2. Dividing both the numerator and the denominator by 2, we get:
(4 ÷ 2) / (6 ÷ 2) = 2/3
Therefore, the simplified fraction representing 4 divided by 6 is 2/3. This means that 4 out of 6 is equivalent to 2 out of 3.
Different Representations of 4/6
It's important to understand that 4/6, 2/3, and even decimal representation (0.666...) all represent the same quantity. The choice of which representation to use depends on the context. Fractions are often preferred in mathematical calculations, especially when dealing with proportions and ratios. Decimals are commonly used in everyday contexts like money and measurements.
Real-World Examples
Let's consider some real-world scenarios where understanding 4/6 (or its simplified form, 2/3) is crucial:
-
Baking: If a recipe calls for 6 cups of flour and you only want to make ⅔ of the recipe, you would use 4 cups of flour (4/6 = 2/3 of 6).
-
Sharing: If you have 6 candies and want to share them equally among 3 friends, each friend would receive 2 candies (4/6 simplified to 2/3; 2/3 of 6 = 4).
-
Measurement: If a project requires a length of 6 meters and you've completed 4 meters, you've finished ⅔ of the project (4/6 = 2/3).
Practice Problems
To solidify your understanding, let's work through some practice problems:
-
Express 8 divided by 12 as a fraction and simplify it to its lowest terms.
- Solution: 8/12 simplifies to 2/3. (GCD of 8 and 12 is 4.)
-
What fraction represents 10 divided by 15? Simplify the fraction.
- Solution: 10/15 simplifies to 2/3. (GCD of 10 and 15 is 5.)
-
If you have a 6-meter rope and use 4 meters, what fraction of the rope did you use? Express your answer in simplest form.
- Solution: 4/6, which simplifies to 2/3.
-
A pizza is cut into 12 slices. You eat 8 slices. What fraction of the pizza did you eat? Simplify your answer.
- Solution: 8/12, which simplifies to 2/3.
Further Exploration: Equivalent Fractions
Understanding equivalent fractions is essential when working with fractions. Equivalent fractions represent the same value but have different numerators and denominators. For example, 4/6, 8/12, and 2/3 are all equivalent fractions. They all represent the same portion of a whole. You can find equivalent fractions by multiplying or dividing both the numerator and denominator by the same number (other than zero).
Connecting Division to Fractions: A Deeper Dive
The process of dividing a number and expressing the result as a fraction highlights the inherent relationship between division and fractions. Division essentially asks, "How many times does the divisor fit into the dividend?" The resulting fraction provides a precise answer, expressing the quotient as a part of a whole. This is particularly important when the division results in a non-whole number, as the fraction provides a clear and concise representation.
Converting Fractions to Decimals and Percentages
While fractions provide a clear representation of parts of a whole, it is sometimes useful to convert fractions into decimals or percentages for easier comparison and interpretation. To convert a fraction to a decimal, simply divide the numerator by the denominator. In the case of 2/3, dividing 2 by 3 gives approximately 0.6667. To convert a decimal to a percentage, multiply it by 100. This would result in approximately 66.67%.
Conclusion
Expressing 4 divided by 6 as a fraction and simplifying it to its lowest terms (2/3) is a foundational concept in mathematics. Understanding this process requires a grasp of division, fractions, and simplification techniques. By mastering these concepts, you can effectively solve a variety of problems involving ratios, proportions, and parts of a whole, whether in mathematical calculations or real-world applications. Remember to always simplify your fractions to their lowest terms for clarity and efficiency. The examples and practice problems provided throughout this guide should reinforce your understanding and equip you to confidently tackle similar problems in the future. Through consistent practice and exploration of related concepts, you'll strengthen your mathematical skills and broaden your understanding of fundamental arithmetic operations.
Latest Posts
Latest Posts
-
Which Is Bigger A Millimeter Or A Centimeter
Jul 26, 2025
-
What Year Was I Born In If Im 14
Jul 26, 2025
-
How Many Tablespoons Is 3 Oz Of Butter
Jul 26, 2025
-
What Is The Gcf Of 14 And 49
Jul 26, 2025
-
Is A Peach Rotting A Chemical Or Physical Change
Jul 26, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.