4 Is What Percent Of 30
Kalali
Apr 27, 2025 · 5 min read
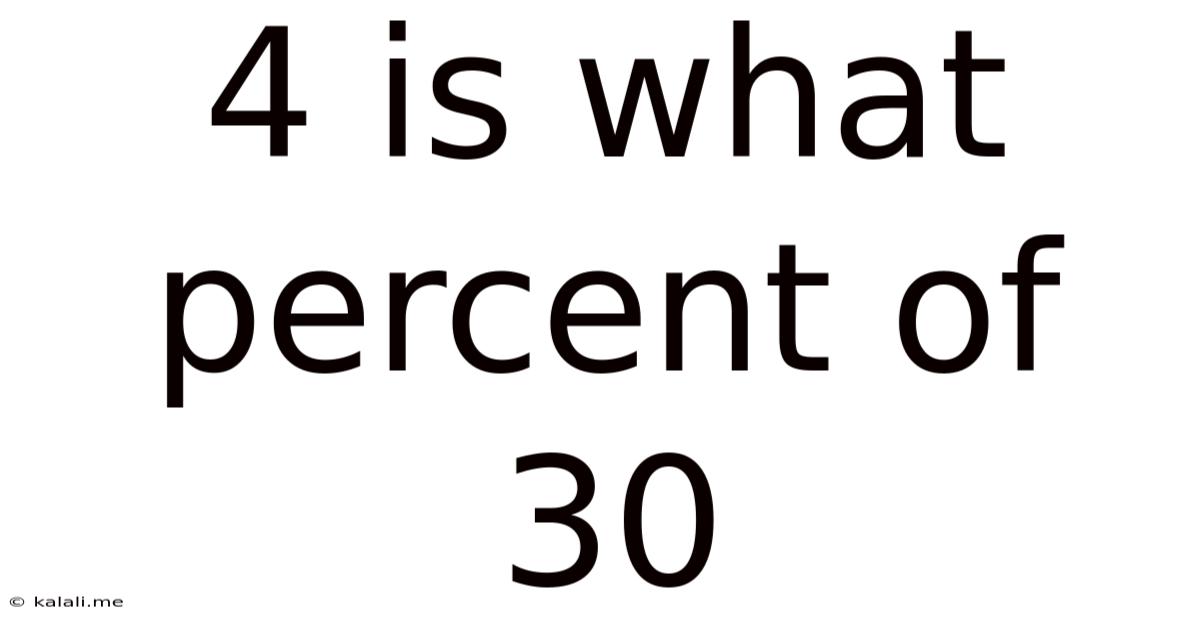
Table of Contents
4 is What Percent of 30? A Deep Dive into Percentage Calculations and Real-World Applications
This seemingly simple question, "4 is what percent of 30?", opens the door to a surprisingly vast world of mathematical concepts and practical applications. Understanding how to solve this problem unlocks the ability to calculate percentages across numerous fields, from finance and budgeting to sales, statistics, and even baking! This article will not only provide the solution but will also delve into the underlying principles, explore different calculation methods, and showcase real-world scenarios where this type of percentage calculation is crucial. By the end, you'll not only know the answer but also possess a solid understanding of percentage calculations and their importance.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." When we say "4 is what percent of 30," we're essentially asking: what fraction of 30 is 4, expressed as a number out of 100? This seemingly simple question underlies countless calculations in everyday life.
Method 1: The Direct Formula Approach
The most straightforward method involves using a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 4
- Whole: 30
Plugging these values into the formula, we get:
(4 / 30) * 100 = 13.33% (approximately)
Therefore, 4 is approximately 13.33% of 30.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion:
4/30 = x/100
Here:
- 4 represents the part.
- 30 represents the whole.
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
30x = 400
x = 400 / 30
x = 13.33% (approximately)
This method reinforces the concept that percentages are simply ratios expressed as parts of 100.
Method 3: Step-by-Step Breakdown for Clarity
Let's break down the calculation into simpler steps for a clearer understanding:
-
Find the decimal equivalent: Divide the part (4) by the whole (30): 4 ÷ 30 = 0.1333...
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.1333... * 100 = 13.33% (approximately)
This step-by-step approach can be particularly helpful for those new to percentage calculations. It emphasizes the relationship between decimals and percentages, crucial for understanding more complex percentage problems.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is invaluable in a wide range of real-world situations. Let's explore a few examples:
1. Finance and Budgeting:
- Calculating interest: Understanding percentages is essential for calculating simple and compound interest on loans, savings accounts, and investments. For example, calculating the interest earned on a savings account requires determining what percentage of the principal amount is earned as interest over a given period.
- Analyzing financial statements: Financial statements, such as balance sheets and income statements, are filled with percentages. Analyzing these percentages helps in understanding profitability, liquidity, and other key financial aspects of a business or individual.
- Budgeting and expense tracking: Tracking expenses and comparing them to income requires calculating percentages. For instance, calculating what percentage of your income goes towards housing, transportation, or food helps you understand your spending habits and make necessary adjustments.
2. Sales and Marketing:
- Calculating discounts and markups: Businesses use percentages to calculate discounts during sales and markups to determine the selling price of products. Understanding these calculations is vital for both businesses and consumers.
- Analyzing sales performance: Sales teams track their performance using percentages. For example, conversion rates (the percentage of leads that convert into sales) and customer retention rates are crucial metrics for evaluating success.
- Commission calculations: Many salespeople earn commissions based on a percentage of their sales. Calculating these commissions accurately is essential for fair compensation.
3. Statistics and Data Analysis:
- Calculating percentages in surveys and polls: Surveys and polls often present results as percentages. For example, understanding the percentage of respondents who favor a particular political candidate is crucial for political analysis.
- Representing data visually: Percentages are commonly used in charts and graphs to represent data visually, making it easier to understand complex information at a glance.
- Determining probabilities: In probability theory, percentages are used to express the likelihood of an event occurring. Understanding these probabilities is crucial in various fields, including insurance and risk management.
4. Everyday Life:
- Calculating tips: Calculating tips in restaurants often involves determining a percentage of the total bill.
- Understanding sales tax: Sales tax is a percentage added to the price of goods and services.
- Cooking and baking: Recipes sometimes require adjusting ingredient amounts based on percentages. For example, increasing a recipe by 50% requires understanding and applying percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While "4 is what percent of 30?" is a fundamental percentage problem, it forms the basis for understanding more complex scenarios:
- Percentage increase and decrease: Calculating the percentage change between two values requires understanding the initial and final values and applying the appropriate formula.
- Compound percentages: Compound interest and other compound percentage problems involve repeated percentage calculations, often over time. Understanding this concept is essential for long-term financial planning.
- Percentage points: Distinguishing between percentage points and percentages is crucial for accurate interpretation of data. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the initial value.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill applicable across diverse areas of life. Understanding the fundamental principles, as demonstrated with the problem "4 is what percent of 30?", empowers you to tackle more complex percentage problems and confidently interpret data in various contexts. From managing personal finances to analyzing business performance, the ability to calculate percentages efficiently and accurately is an asset that significantly enhances decision-making capabilities. Remember the simple formula, the proportion method, or the step-by-step approach – choose the method that best suits your understanding and confidently tackle any percentage challenge that comes your way. The ability to understand and calculate percentages isn't just about numbers; it's about understanding the world around you a little bit better.
Latest Posts
Latest Posts
-
How Many Covalent Bonds Can A Carbon Atom Form
Apr 28, 2025
-
How Many Litres Is 55 Gallons
Apr 28, 2025
-
What Is The Percentage Of 11 Out Of 13
Apr 28, 2025
-
What Is A Multiple Of 18
Apr 28, 2025
-
What Is 1 16 As A Percent
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.