4 Is What Percent Of 40
Kalali
Apr 22, 2025 · 5 min read
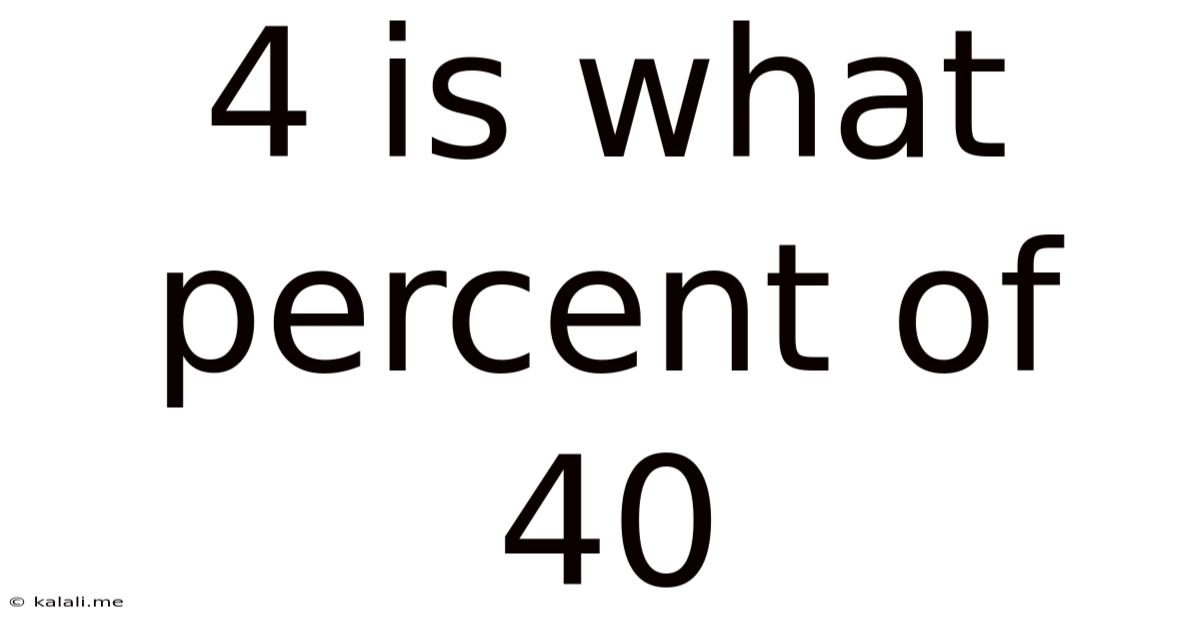
Table of Contents
4 is What Percent of 40? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "4 is what percent of 40?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. Understanding percentages is fundamental to numerous aspects of daily life, from calculating discounts and taxes to analyzing financial data and understanding statistics. This article will not only answer the initial question but also delve into the methods for solving percentage problems, exploring different approaches and highlighting their relevance in various real-world scenarios.
Meta Description: Discover how to calculate percentages and understand the practical applications of percentage calculations, using the example "4 is what percent of 40?". This comprehensive guide explains various methods and real-world scenarios.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental concept is crucial for solving any percentage problem.
We often use percentages to compare quantities, represent proportions, or show changes over time. For example, a 20% discount means you save 20 out of every 100 units of currency, a 5% increase in salary means your income has grown by 5 units for every 100 units of your previous salary, and a 15% market share means that a company controls 15 out of every 100 units of the market.
Solving "4 is What Percent of 40?"
Let's now tackle the core question: "4 is what percent of 40?" There are several ways to approach this problem:
Method 1: Using the Proportion Method
This method relies on setting up a proportion. We can represent the problem as:
4/40 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
4 * 100 = 40 * x
400 = 40x
x = 400/40
x = 10
Therefore, 4 is 10% of 40.
Method 2: Using the Decimal Method
This method involves converting the fraction 4/40 into a decimal and then multiplying by 100 to express it as a percentage.
First, we simplify the fraction:
4/40 = 1/10 = 0.1
Then, we multiply the decimal by 100:
0.1 * 100 = 10%
Again, we arrive at the answer: 4 is 10% of 40.
Method 3: Using the Formula Method
A more direct formula can be used:
Percentage = (Part/Whole) * 100
In this case, the "part" is 4, and the "whole" is 40. Plugging these values into the formula:
Percentage = (4/40) * 100 = 0.1 * 100 = 10%
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations. Here are just a few examples:
1. Retail and Sales: Calculating discounts, sales tax, and profit margins are all heavily reliant on percentage calculations. Understanding these calculations allows consumers to make informed purchasing decisions and businesses to manage their finances effectively. For instance, a 25% discount on a $100 item means a savings of $25, resulting in a final price of $75.
2. Finance and Investing: Percentages are crucial in finance for calculating interest rates, returns on investment, and analyzing financial statements. Understanding percentage change helps investors track the performance of their investments and make informed decisions about their portfolio. A 10% increase in the value of a stock signifies a positive growth, while a 5% decrease indicates a loss.
3. Statistics and Data Analysis: Percentages are frequently used to represent proportions and trends in data. For instance, analyzing survey results, understanding demographic data, or evaluating the success rate of a marketing campaign all involve working with percentages. A 70% approval rating in a survey suggests strong public support.
4. Science and Measurement: In scientific fields, percentages are used to express concentrations, errors, and other measurements. For example, a 5% solution means that 5 parts of the solute are dissolved in 95 parts of the solvent, resulting in a total of 100 parts.
5. Everyday Life: From calculating tips in restaurants to understanding nutrition labels on food products, percentages are ubiquitous in our daily lives. A 15% tip on a $50 meal amounts to $7.50. Knowing the percentage of daily recommended values of nutrients helps us to manage our health effectively.
Beyond the Basics: More Complex Percentage Problems
While "4 is what percent of 40?" is a relatively simple problem, understanding percentages extends to more complex scenarios:
1. Percentage Increase and Decrease: Calculating the percentage increase or decrease between two values requires understanding the initial and final values. For instance, if a salary increases from $50,000 to $55,000, the percentage increase is calculated as: [(55000 - 50000)/50000] * 100 = 10%. Similarly, a decrease is calculated using the same formula.
2. Compound Interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. This concept is frequently used in savings accounts and loans, making it crucial for financial planning. The formula for compound interest involves percentages and exponential growth.
3. Percentage Points: It’s important to distinguish between percentage change and percentage points. A change from 10% to 20% represents a 10 percentage point increase, but a 100% percentage increase. This distinction is important for accurate interpretation of data.
Developing Proficiency in Percentage Calculations
Mastering percentage calculations requires practice and a solid understanding of the underlying mathematical concepts. Here are some tips for improving your skills:
- Practice regularly: Solve various percentage problems with increasing complexity.
- Use different methods: Familiarize yourself with various approaches like the proportion method, decimal method, and formula method.
- Check your answers: Verify your calculations to ensure accuracy.
- Use online resources: Explore websites and educational platforms that offer practice problems and tutorials on percentages.
- Apply percentages to real-world scenarios: Relate percentage calculations to real-life situations to enhance understanding and retention.
Conclusion
The seemingly simple question, "4 is what percent of 40?", serves as a gateway to a comprehensive understanding of percentages and their widespread applications. From everyday calculations to complex financial analyses, the ability to calculate and interpret percentages is a fundamental skill with far-reaching implications. By mastering the methods and understanding the concepts explained in this article, you can confidently tackle a wide range of percentage problems and apply this knowledge effectively in various aspects of your life. Remember to practice regularly, explore different approaches, and relate the concepts to real-world scenarios to truly solidify your understanding.
Latest Posts
Latest Posts
-
Cuanto Es 7 Metros En Pies
Apr 23, 2025
-
How Many Kilometers Are In 7 Miles
Apr 23, 2025
-
Greatest Common Factor Of 12 And 8
Apr 23, 2025
-
What Is 3 20 As A Decimal
Apr 23, 2025
-
What Is The Least Common Multiple Of 18 12
Apr 23, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.