4 Out Of 6 As A Percentage
Kalali
Apr 17, 2025 · 5 min read
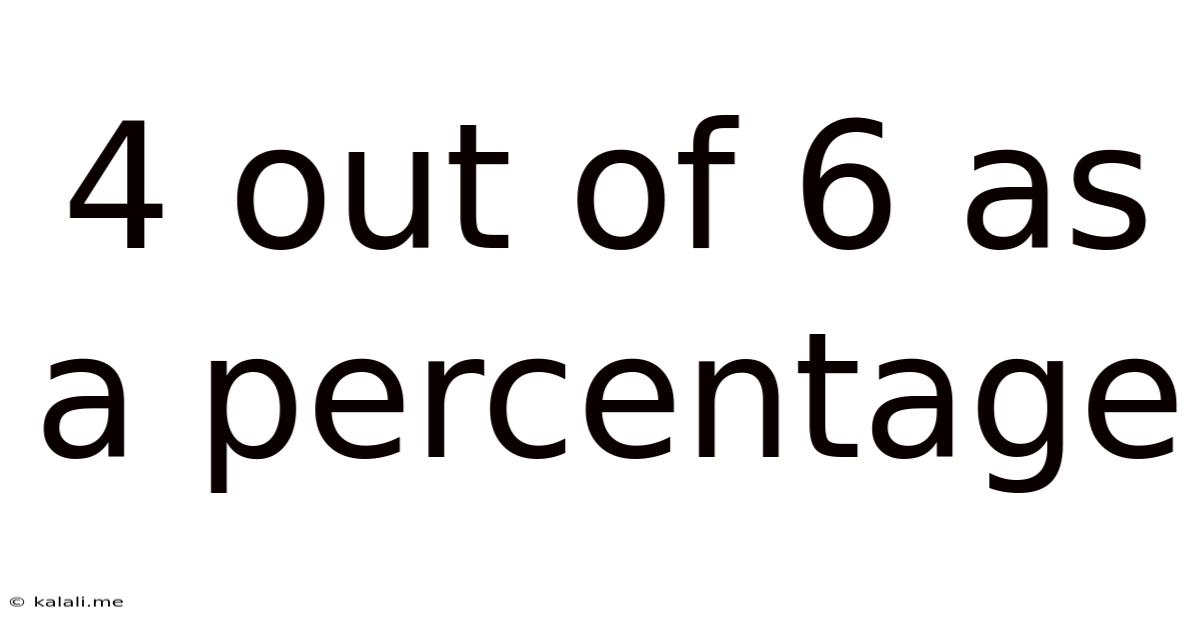
Table of Contents
4 out of 6 as a Percentage: A Comprehensive Guide to Fraction-to-Percentage Conversion
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific analyses and business projections. Understanding how to convert fractions into percentages is particularly crucial. This article provides a comprehensive guide on determining what 4 out of 6 represents as a percentage, along with various methods and practical applications. We'll also explore related percentage calculations and offer tips for improving your understanding of this important mathematical concept.
What is a Percentage?
Before diving into the calculation, let's clarify the concept of a percentage. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred," indicated by the symbol "%". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: The Direct Conversion Method
The most straightforward approach to converting 4 out of 6 into a percentage involves expressing the fraction as a decimal and then multiplying by 100.
-
Express the fraction: The statement "4 out of 6" is represented as the fraction 4/6.
-
Simplify the fraction (optional but recommended): We can simplify 4/6 by dividing both the numerator (top number) and the denominator (bottom number) by their greatest common divisor, which is 2. This simplifies the fraction to 2/3. Simplifying the fraction makes the subsequent calculations easier.
-
Convert the fraction to a decimal: Divide the numerator by the denominator: 2 ÷ 3 ≈ 0.6667 (we'll round to four decimal places for accuracy).
-
Multiply by 100 to express as a percentage: 0.6667 x 100 = 66.67%
Therefore, 4 out of 6 is equal to 66.67%.
Method 2: The Proportion Method
This method uses proportions to solve for the percentage. We set up a proportion where one ratio represents the fraction (4/6) and the other represents the percentage (x/100), where 'x' is the unknown percentage.
-
Set up the proportion: 4/6 = x/100
-
Cross-multiply: 4 * 100 = 6 * x This simplifies to 400 = 6x
-
Solve for x: Divide both sides of the equation by 6: x = 400/6 ≈ 66.67
Therefore, x ≈ 66.67%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function. You can directly input the fraction as a division (4 ÷ 6) and then multiply the result by 100 to obtain the percentage. This is the quickest method, especially for more complex fractions.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in many real-world scenarios:
-
Academic Performance: Calculating grades often involves converting the number of correct answers to a percentage. For example, if a student gets 4 out of 6 questions correct on a quiz, their score is 66.67%.
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. Understanding percentages allows consumers to quickly calculate the final price after a discount.
-
Financial Calculations: Percentages are fundamental in finance, used for calculating interest rates, tax rates, profit margins, and investment returns.
-
Data Analysis and Statistics: Percentages are used extensively in data analysis to represent proportions, trends, and distributions within datasets. For instance, expressing survey results as percentages makes them easier to interpret and compare.
-
Scientific Research: In scientific experiments and studies, percentages are used to express experimental error, success rates, and changes in measured variables.
Understanding Related Percentage Calculations
Mastering the conversion of 4 out of 6 to a percentage helps build a foundation for solving other related problems. Here are some examples:
-
Finding a percentage of a number: If you need to find 66.67% of a larger number (e.g., 66.67% of 150), you simply multiply the number by the decimal equivalent of the percentage (0.6667 * 150 = 100).
-
Calculating percentage increase or decrease: This involves determining the percentage change between two numbers. For instance, if a quantity increases from 60 to 80, the percentage increase is calculated as [(80-60)/60] * 100 = 33.33%.
-
Determining the original value from a percentage: If you know a percentage and the resulting value, you can work backward to find the original value. For example, if 66.67% of a number is 100, the original number is 100 / 0.6667 ≈ 150.
Improving Your Understanding of Percentages
To improve your understanding and skills in calculating percentages:
-
Practice regularly: The more you practice converting fractions to percentages and performing related calculations, the more confident and proficient you'll become.
-
Use different methods: Try all the methods outlined in this article (direct conversion, proportion, and calculator) to find the one that best suits your preference and the specific problem.
-
Visual aids: Utilize visual aids like pie charts or bar graphs to represent percentages and build a better intuitive understanding.
-
Real-world applications: Apply your knowledge to real-world problems to reinforce your understanding and see the practical relevance of percentage calculations.
-
Online resources: Explore online resources, such as educational websites and videos, that provide further explanations and practice exercises.
Conclusion:
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. We've demonstrated multiple ways to calculate 4 out of 6 as a percentage, resulting in approximately 66.67%. Understanding this concept and related percentage calculations is crucial for success in various academic, professional, and personal endeavors. By practicing consistently and utilizing the strategies outlined in this guide, you can master percentage calculations and confidently apply them to a wide range of situations. Remember that accuracy is key, and understanding the underlying principles will allow you to tackle more complex percentage problems with ease. Continuous practice and a focus on understanding the "why" behind the calculations will lead to a solid grasp of this vital mathematical concept.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 3 4 5
Apr 19, 2025
-
What 2 Planets Have No Moons
Apr 19, 2025
-
What Is 5 7 As A Decimal
Apr 19, 2025
-
20 Of What Number Is 16
Apr 19, 2025
-
How Long Is 75cm In Inches
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 6 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.