4 To The Power Of 12
Kalali
Apr 03, 2025 · 5 min read
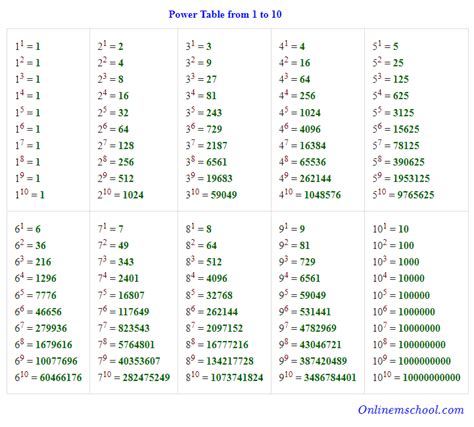
Table of Contents
4 to the Power of 12: Unveiling the Magnitude and Applications
4 to the power of 12, often written as 4<sup>12</sup> or 4**12, represents a significant number with far-reaching implications across various fields. This article delves deep into the calculation, significance, and real-world applications of this mathematical concept. We will explore its numerical value, its representation in different systems, and how it manifests in various scientific, technological, and even everyday contexts.
Calculating 4 to the Power of 12
The expression 4<sup>12</sup> signifies that the base number 4 is multiplied by itself twelve times. This can be written as: 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4 x 4. While manually calculating this might seem tedious, calculators and programming languages readily provide the solution. The result is a substantial number: 16,777,216.
This seemingly simple calculation has profound implications when we consider its application in different areas. Let's explore some of them.
Representing 4 to the Power of 12: Different Number Systems
Understanding 4<sup>12</sup> extends beyond its decimal representation. Let's examine how it's represented in other number systems:
Binary Representation
The binary system, fundamental to computer science, uses only two digits: 0 and 1. Converting 16,777,216 to binary requires repeated division by 2. The binary representation of 4<sup>12</sup> is 1000000000000000000. This highlights the efficiency of exponential notation in representing large numbers, even in binary, where space is a critical factor.
Hexadecimal Representation
Hexadecimal, a base-16 system, uses digits 0-9 and letters A-F (representing 10-15). Hexadecimal is commonly used in computer programming to represent memory addresses and color codes. The hexadecimal representation of 16,777,216 is 1000000. Notice how concise this representation is compared to its binary or decimal counterparts.
Scientific Notation
For very large numbers, scientific notation offers a compact and convenient representation. 16,777,216 in scientific notation is 1.6777216 x 10<sup>7</sup>. This representation emphasizes the order of magnitude, making it easier to compare and understand extremely large numbers.
Applications of 4 to the Power of 12
The number 16,777,216, stemming from 4<sup>12</sup>, surfaces in diverse applications:
Computer Science and Data Structures
-
Addressing: In computer systems with a 24-bit address bus, the maximum number of memory addresses possible is 2<sup>24</sup>, which is 16,777,216. This number dictates the amount of directly addressable memory.
-
Color Representation: With 24-bit color depth (often referred to as "true color"), each pixel can display one of 16,777,216 different colors (2<sup>24</sup>). This large color palette allows for rich and realistic image representation.
-
Data Structures: Certain data structures, like arrays or grids, might have dimensions related to powers of 2 for efficient memory management and access. A 4096 x 4096 (4096 = 2<sup>12</sup>) pixel image, for instance, would require 16,777,216 individual pixels.
Combinatorics and Probability
Combinatorial problems frequently involve calculations related to powers. Consider scenarios involving choosing items from a set: If you have four options, and you need to make twelve independent choices, the total number of possible combinations would involve a power of 4. While not exactly 4<sup>12</sup> in all cases (depending on whether repetition is allowed), it demonstrates the potential for exponential growth in such problems.
Finance and Compound Interest
Compound interest calculations involve exponential growth. While not directly related to 4<sup>12</sup> in a typical scenario, the principle of exponential growth highlights how small increases can lead to substantial returns over time. Understanding exponential growth is crucial in financial planning and investment strategies.
Other Applications
-
Games and Simulations: Game developers might use numbers like 4<sup>12</sup> to represent the number of possible game states or scenarios in complex simulations.
-
Engineering and Physics: In certain physics and engineering models, calculations might involve raising numbers to powers for modeling various phenomena. While 4<sup>12</sup> might not be a common constant, the understanding of exponential relationships is crucial.
-
Cryptography: Cryptography relies heavily on large numbers and their properties. While not directly using 4<sup>12</sup>, the understanding of exponential functions is fundamental for creating secure cryptographic systems.
Understanding Exponential Growth
The concept of exponential growth is central to understanding the significance of 4<sup>12</sup>. Exponential growth refers to an increase in quantity over time, where the rate of growth is proportional to the current value. This leads to rapid increases, as seen with 4<sup>12</sup>. In contrast, linear growth increases at a constant rate. The difference between these two types of growth becomes dramatically apparent as the exponent increases.
Comparing Exponential and Linear Growth
Let's compare the growth of 4<sup>x</sup> (exponential) to 4x (linear) for different values of x:
| x | 4<sup>x</sup> | 4x |
|---|---|---|
| 1 | 4 | 4 |
| 2 | 16 | 8 |
| 3 | 64 | 12 |
| 4 | 256 | 16 |
| 5 | 1024 | 20 |
| 10 | 1,048,576 | 40 |
| 12 | 16,777,216 | 48 |
This table clearly illustrates the vast difference in magnitude between exponential and linear growth. The exponential function (4<sup>x</sup>) increases far more rapidly than the linear function (4x). This difference becomes even more pronounced as x increases.
Conclusion
4 to the power of 12, resulting in 16,777,216, is more than just a numerical value. It's a concept with widespread applications in computer science, combinatorics, finance, and various other fields. Understanding its calculation, representations in different number systems, and implications for exponential growth provides valuable insight into the power and versatility of mathematical concepts in diverse real-world applications. Its significance lies not only in its numerical magnitude but also in the fundamental principles of exponential growth and its profound influence on various aspects of science, technology, and beyond. The seemingly simple calculation of 4<sup>12</sup> opens a window to a world of complex systems and exponential possibilities.
Latest Posts
Latest Posts
-
How Can A Change In Technology Affect Scientific Knowledge
Apr 03, 2025
-
How Much Is 19 Celsius In Fahrenheit
Apr 03, 2025
-
What Are The Three Main Weapons Of Predators
Apr 03, 2025
-
How Many Phosphate Groups Does Atp Have
Apr 03, 2025
-
What Is 300 F In C
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 4 To The Power Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
