40 Is What Percent Of 180
Kalali
Apr 27, 2025 · 5 min read
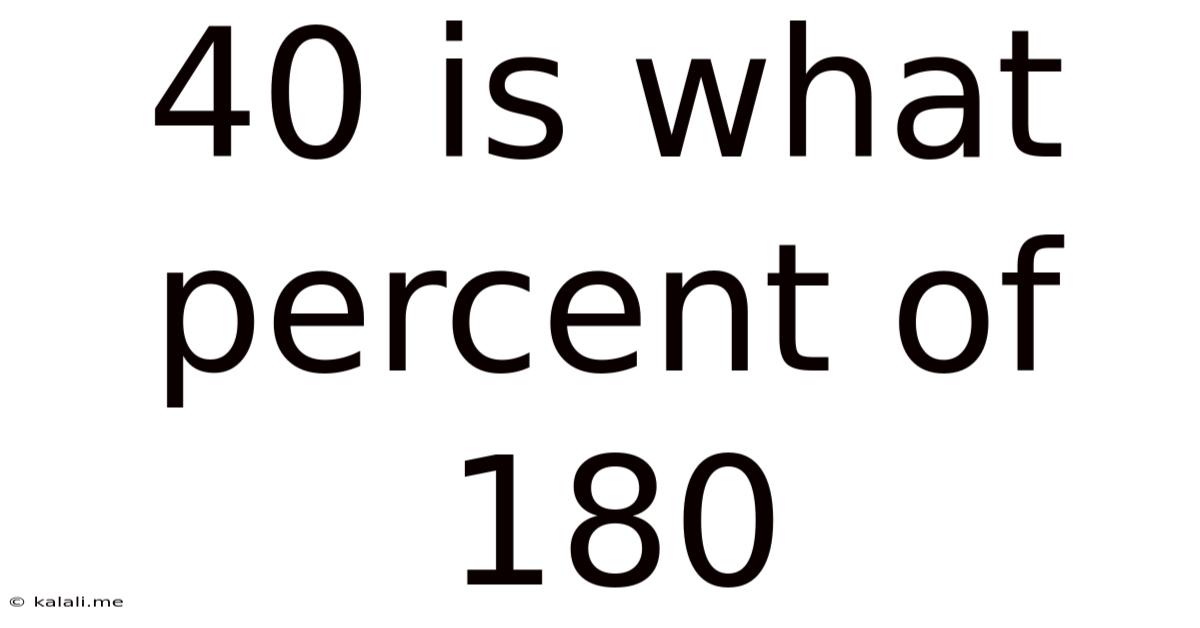
Table of Contents
40 is What Percent of 180? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "40 is what percent of 180?" – opens the door to understanding a fundamental mathematical concept crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistics and data analysis. This comprehensive guide will not only answer the question directly but also delve into the underlying principles, provide multiple methods for solving similar problems, and explore practical real-world examples.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to solve "40 is what percent of 180?". This guide covers multiple methods, real-world examples, and expands on percentage calculation concepts.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5. Understanding this basic definition is key to mastering percentage calculations.
Method 1: The Formulaic Approach
The most straightforward method to find what percentage 40 represents of 180 is using the following formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 40 (the number we want to express as a percentage)
- Whole: 180 (the total number)
Substituting these values into the formula:
(40 / 180) * 100 = 22.22% (approximately)
Therefore, 40 is approximately 22.22% of 180.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion equates two ratios. We can set up a proportion to solve for the unknown percentage (x):
40/180 = x/100
To solve for x, we cross-multiply:
40 * 100 = 180 * x
4000 = 180x
x = 4000 / 180
x ≈ 22.22
Again, we arrive at the answer: 40 is approximately 22.22% of 180.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction:
40/180
Simplify the fraction (optional but helpful):
2/9
Convert the fraction to a decimal by dividing the numerator by the denominator:
2 ÷ 9 ≈ 0.2222
Multiply the decimal by 100 to express it as a percentage:
0.2222 * 100 ≈ 22.22%
This method confirms that 40 is approximately 22.22% of 180.
Real-World Applications: Putting Percentages to Work
Understanding percentage calculations is essential for navigating various aspects of daily life. Here are some practical examples:
-
Sales and Discounts: Imagine a store offers a 25% discount on an item originally priced at $180. To calculate the discount, you would find 25% of 180: (25/100) * 180 = $45. The sale price would be $180 - $45 = $135.
-
Taxes: If the sales tax in your area is 6%, and you purchase an item for $40, you'd calculate the tax as: (6/100) * 40 = $2.40. The total cost would be $40 + $2.40 = $42.40.
-
Grade Calculation: Suppose you scored 40 points out of a possible 180 points on a test. Your percentage score would be: (40/180) * 100 ≈ 22.22%.
-
Financial Analysis: Investors often use percentages to assess returns on investments, growth rates, and market share. Understanding percentage changes is crucial for making informed financial decisions.
-
Data Interpretation: Many statistical analyses and data visualizations utilize percentages to represent proportions and trends within data sets. For example, understanding the percentage of a population that holds a certain opinion is essential for market research and political polling.
-
Tip Calculation: Calculating a tip at a restaurant frequently involves percentages. For instance, a 15% tip on a $40 meal would be (15/100) * 40 = $6.
Expanding on Percentage Calculations: Advanced Concepts
While the basic percentage formula is fundamental, several related concepts extend its application:
-
Percentage Increase/Decrease: Calculating the percentage change between two values involves finding the difference between the values, dividing by the original value, and then multiplying by 100. For instance, if a value increases from 100 to 120, the percentage increase is: [(120-100)/100] * 100 = 20%.
-
Finding the Original Value: If you know the percentage and the resulting value after a percentage increase or decrease, you can work backward to find the original value. This often requires using algebraic equations.
-
Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest. This leads to exponential growth over time and requires more complex calculations.
-
Percentage Points: It's crucial to distinguish between percentage points and percentage change. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original value.
Troubleshooting Common Errors in Percentage Calculations
Several common errors can arise when working with percentages:
-
Incorrect Formula Application: Ensure you're using the correct formula for the specific problem you're solving. Double-check your substitutions of values into the formula.
-
Rounding Errors: Rounding off numbers too early in the calculation can lead to inaccurate final results. It's best to maintain accuracy until the final step.
-
Confusion between Percentage Points and Percentage Change: Clearly distinguish between these two concepts to avoid misinterpretations.
-
Misunderstanding the "Whole": Correctly identifying the "whole" or the total amount is crucial. The "whole" is the base upon which the percentage is calculated.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "40 is what percent of 180?", serves as a gateway to a deeper understanding of percentages and their widespread applications. By mastering the various methods outlined in this guide and understanding the associated concepts, you'll be equipped to confidently tackle percentage calculations in diverse real-world scenarios, from managing your finances to interpreting data and making informed decisions. Remember to practice regularly to solidify your understanding and develop proficiency in this essential mathematical skill. The more you practice, the easier and more intuitive percentage calculations will become. This skill will undoubtedly prove invaluable in both your personal and professional life.
Latest Posts
Latest Posts
-
How Does Mercury Differ From Other Metals
Apr 27, 2025
-
What Is 135 Degrees Celsius In Fahrenheit
Apr 27, 2025
-
Is Cold Water Denser Than Warm Water
Apr 27, 2025
-
What Is The Square Root Of 109
Apr 27, 2025
-
What Is 25 Degrees Fahrenheit In Celsius
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about 40 Is What Percent Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.